Плоскость в пространстве

Всякий (не равный нулю) вектор, перпендикулярный к данной плоскости, называется её нормальным вектором.

Уравнение плоскости, проходящей через точку M₀ (x₀; y₀; z₀) и имеющей нормальный вектор 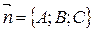: 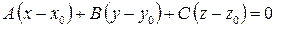(1)

Общее уравнение: 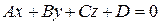(2)

Уравнение плоскости в отрезках: 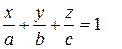(3)

Угол 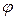между плоскостями 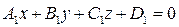и :

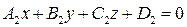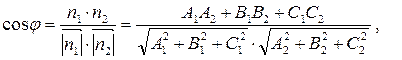(4)

Условие параллельности плоскостей:

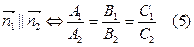
Условие перпендикулярности плоскостей:

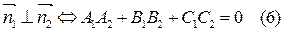
Уравнение плоскости, проходящей через три заданные точки

M₁ (x₁; y₁; z₁), M₂ (x₂; y₂; z₂), M₃ (x₃; y₃; z₃):

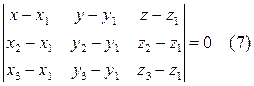
Нормальным уравнением плоскости: 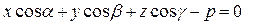(8)

где 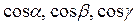– направляющие косинусы нормали плоскости,

p – расстояние от начала координат до плоскости.

Для перехода от общего уравнения плоскости 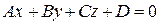к нормальному находим нормирующий множитель 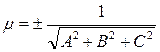, знак которого противоположен знаку свободного члена общего уравнения.

Расстояние d от точки до плоскости: 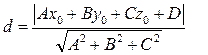(9)