Тема. Плоскость. Различные виды уравнений плоскости. Расстояние от точки до плоскости.
Тема. Прямая в пространстве. Различные виды уравнений прямой в пространстве. Взаимное расположение прямой и плоскости.
3.70 Написать уравнение плоскости 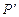 , проходящей через заданные точки
, проходящей через заданные точки 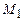 и
и 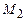 перпендикулярно заданной плоскости
перпендикулярно заданной плоскости 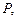 если:
если:
а) 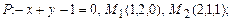 б)
б) 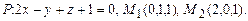
3.71 Написать уравнение плоскости, проходящей через точку 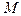 параллельно векторам
параллельно векторам 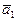 и
и 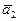 , если:
, если:
а) 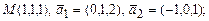 б)
б) 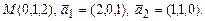
3.72 Написать уравнение плоскости, проходящей через точки 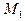 и
и 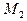 параллельно вектору
параллельно вектору 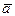 , если:
, если:
а) 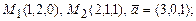 б)
б) 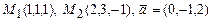 .
.
3.73 Написать уравнение плоскости, проходящей через три заданные точки 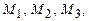 если:
если:
а) 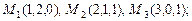 б)
б) 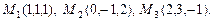
3.74 Написать уравнение плоскости, зная, что точка 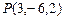 служит основанием перпендикуляра, опущенного из начала координат на эту плоскость.
служит основанием перпендикуляра, опущенного из начала координат на эту плоскость.
3.75 Составить уравнение плоскости: а) проходящей через точку 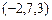 параллельно плоскости
параллельно плоскости 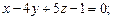 б) проходящей через начало координат и перпендикулярной к двум плоскостям:
б) проходящей через начало координат и перпендикулярной к двум плоскостям: 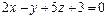 и
и 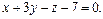
3.76 Написать уравнение плоскости: а) параллельной плоскости 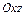 и проходящей через точку
и проходящей через точку 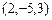 ; б) проходящей через ось
; б) проходящей через ось 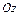 и через точку
и через точку 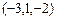 ; в) параллельной оси О x и проходящей через две точки
; в) параллельной оси О x и проходящей через две точки 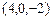 и (5, 1, 7).
и (5, 1, 7).
3.77 Вычислить отрезки, отсекаемые на осях координат плоскостями. Построить плоскости.
а) 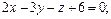 б)
б) 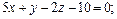 в)
в) 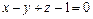 .
.
3.78 Через точку 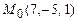 провести плоскость, которая отсекала бы на осях координат положительные и равные между собой отрезки.
провести плоскость, которая отсекала бы на осях координат положительные и равные между собой отрезки.
3.79 Вычислить углы между следующими плоскостями:
а) 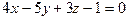 и
и 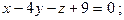 б)
б) 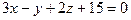 и
и 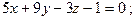
в) 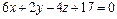 и
и 
3.80 Вычислить расстояние:
а) точки 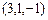 от плоскости
от плоскости 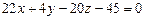 ;
;
б) точки 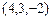 от плоскости
от плоскости 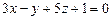 ; в) точки
; в) точки 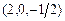 от плоскости
от плоскости 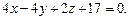
3.81 Вычислить расстояние между плоскостями: 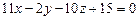 и
и 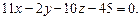
3.82 Найти точку, симметричную с началом координат относительно плоскости 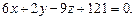
3.83 На оси О z найти точку, равноудаленную от двух плоскостей: 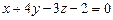 и
и 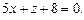
3,84 На расстоянии трех единиц от плоскости 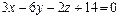 провести параллельную ей плоскость.
провести параллельную ей плоскость.
3.85 Вычислить объем пирамиды, ограниченной плоскостью 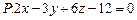 и координатными плоскостями.
и координатными плоскостями.
3.86 Написать уравнение прямой, проходящей через две заданные точки 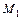 и
и 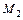 , если:
, если:
а) 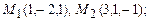 б)
б) 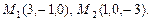
3.87 Прямая L задана общим уравнением. Написать для этой прямой, проходящей через точку
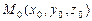 , её каноническое уравнение, если: а)
, её каноническое уравнение, если: а) 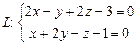 ; б)
; б) 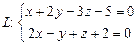 .
.
3.88. Написать каноническое уравнение прямой, проходящей через точку 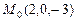 параллельно:
параллельно:
а) вектору 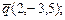 б) прямой
б) прямой 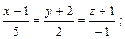 в) оси
в) оси 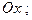 г) оси
г) оси 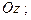 д) прямой
д) прямой 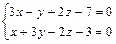 ; е) прямой
; е) прямой 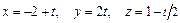 .
.
3.89 Задана прямая 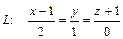 и точка
и точка 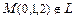 . Требуется: а) написать уравнение плоскости, проходящей через прямую
. Требуется: а) написать уравнение плоскости, проходящей через прямую 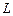 и точку
и точку 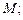 б) написать уравнение плоскости, проходящей через точку
б) написать уравнение плоскости, проходящей через точку 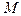 перпендикулярно прямой
перпендикулярно прямой 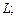 в) вычислить расстояние
в) вычислить расстояние 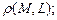
3.90 Заданы плоскость 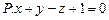 и прямая
и прямая 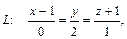 причем
причем 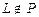 . Требуется:
. Требуется:
а) вычислить 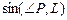 и координаты точки пересечения прямой и плоскости; б) написать уравнение плоскости, проходящей через прямую
и координаты точки пересечения прямой и плоскости; б) написать уравнение плоскости, проходящей через прямую 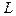 перпендикулярно к плоскости
перпендикулярно к плоскости 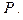
3.91 Найти расстояние от точки 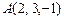 до заданной прямой
до заданной прямой 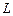 : а)
: а) 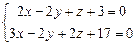 ; б)
; б) 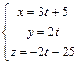 .
.
3.92 При каком значении 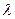 плоскость
плоскость 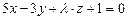 будет параллельна прямой
будет параллельна прямой 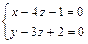 .
.
3.93 Определить угол между прямой 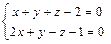 и плоскостью, проходящей через точки
и плоскостью, проходящей через точки 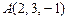 ,
, 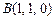 ,
, 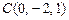 .
.
3.94 Найти расстояние между параллельными прямыми:
а) 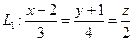 и
и  ; б)
; б) 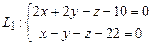 и
и 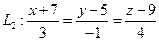 .
.
3.95 Для заданных прямых 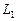 и
и 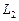 требуется доказать, что прямые не лежат в одной плоскости, т.е. являются скрещивающимися и вычислить расстояние между ними:
требуется доказать, что прямые не лежат в одной плоскости, т.е. являются скрещивающимися и вычислить расстояние между ними:
а) 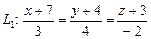 и
и 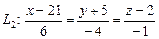 ;
;
б) 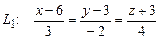 и
и 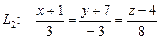 .
.
Ответы:
3.70 а) 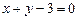 , б)
, б) 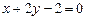 . 3.71 а)
. 3.71 а) 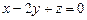 , б)
, б) 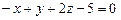 . 3.72 а)
. 3.72 а) 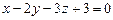 , б)
, б) 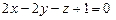 .3.73 а)
.3.73 а) 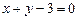 , б)
, б) 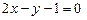 . 3.74
. 3.74 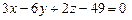 3.75 а)
3.75 а) 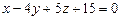 , б)
, б) 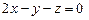 .3.76 а)
.3.76 а) 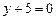 , б)
, б) 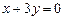 , в)
, в) 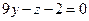 . 3.77 а)
. 3.77 а) 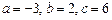 , б)
, б) 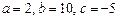 , в)
, в) 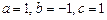 . 3.78
. 3.78 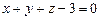 . 3.79 а)
. 3.79 а) 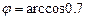 , б)
, б) 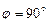 , в)
, в) 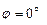 .3.80 а)
.3.80 а) 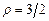 ,б)
,б) 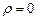 ,в)
,в) 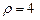 . 3.81
. 3.81 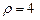 . 3.82
. 3.82 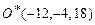 .3.83 M( 0,0,3),
.3.83 M( 0,0,3), 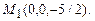 3.84
3.84 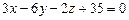 и
и 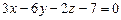 3.85
3.85 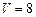 . 3.86 а)
. 3.86 а) 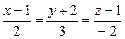 , б)
, б) 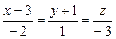 . 3.87 а)
. 3.87 а) 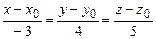 , б)
, б) 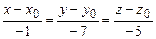 . 3.88 а)
. 3.88 а) 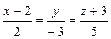 , б)
, б) 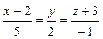 , в)
, в) 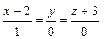 , г)
, г) 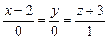 , д)
, д) 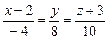 , е)
, е) 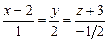 . 3.89 а)
. 3.89 а) 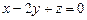 , б)
, б) 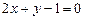 , в).
, в). 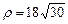 .3.90 а)
.3.90 а) 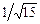
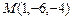 , б)
, б) 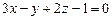 . 3.91 а)
. 3.91 а) 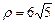 , б)
, б) 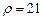 . 3.92
. 3.92 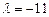 . 3.93
. 3.93 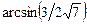 .3.94 а)
.3.94 а) 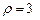 , б)
, б) 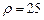 . 3.95 а)
. 3.95 а) 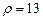 , б)
, б) 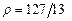 .
.
 2015-06-28
2015-06-28 811
811







