Тема. Прямая на плоскости. Различные виды уравнений прямой на плоскости. Расстояние от точки до прямой. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых на плоскости.
Нормальным вектором прямой 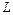 , называется всякий ненулевой вектор
, называется всякий ненулевой вектор 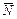 перпендикулярный данной прямой. Направляющим вектором прямой
перпендикулярный данной прямой. Направляющим вектором прямой 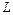 , называется всякий ненулевой вектор
, называется всякий ненулевой вектор 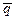 параллельный данной прямой.
параллельный данной прямой.
Прямая 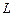 на плоскости в системе координат
на плоскости в системе координат 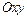 может быть задана уравнением одного из следующих видов:
может быть задана уравнением одного из следующих видов:
1) 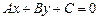 - общее уравнение прямой, где
- общее уравнение прямой, где 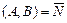 - нормальный вектор прямой;
- нормальный вектор прямой;
2) 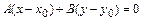 - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку 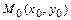 перпендикулярно данному вектору
перпендикулярно данному вектору 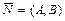 ; 3)
; 3) 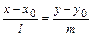 - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку 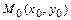 параллельно данному вектору
параллельно данному вектору 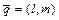 (каноническое уравнение); 4)
(каноническое уравнение); 4) 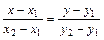 - уравнение прямой, проходящей через две данные точки
- уравнение прямой, проходящей через две данные точки 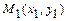 ,
, 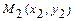 ; 5)
; 5) 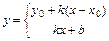 -уравнения прямой с угловым коэффициентом
-уравнения прямой с угловым коэффициентом 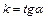 , где
, где 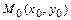 - точка через которую прямая проходит;
- точка через которую прямая проходит; 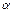 (
(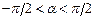 ) – угол, который прямая составляет с осью
) – угол, который прямая составляет с осью 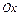 ;
; 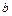 - длина отрезка (со знаком
- длина отрезка (со знаком 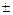 ), отсекаемого прямой на оси
), отсекаемого прямой на оси 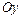 (знак «
(знак «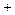 », если отрезок отсекается на положительной части оси и «
», если отрезок отсекается на положительной части оси и «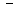 », если на отрицательной). 6)
», если на отрицательной). 6) 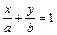 -уравнение прямой в отрезках, где
-уравнение прямой в отрезках, где 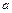 и
и 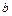 - длины отрезков (со знаком
- длины отрезков (со знаком 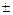 ), отсекаемых прямой на координатных осях
), отсекаемых прямой на координатных осях 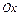 и
и 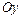 (знак «
(знак «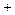 », если отрезок отсекается на положительной части оси и «
», если отрезок отсекается на положительной части оси и «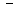 », если на отрицательной).
», если на отрицательной).
Расстояние от точки 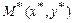 до прямой
до прямой 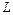 , заданной общим уравнением
, заданной общим уравнением 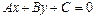 на плоскости, находится по формуле:
на плоскости, находится по формуле: 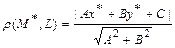 .
.
Угол 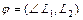 , (
, (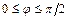 ) между прямыми
) между прямыми 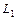 и
и 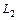 , заданными общими уравнениями или уравнениями с угловым коэффициентом, находится по одной из формул:
, заданными общими уравнениями или уравнениями с угловым коэффициентом, находится по одной из формул: 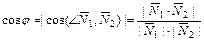 ;
; 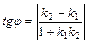 .
.
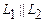 , если
, если 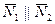
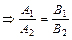 или
или 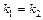 .
.
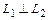 ,если
,если 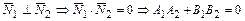 или
или 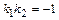
Координаты точки пересечения прямых 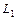 и
и 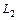 находятся как решение системы линейных уравнений:
находятся как решение системы линейных уравнений:
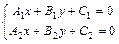 или
или 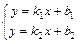 .
.
В задачах 3.1-3.3 требуется написать уравнение прямой, привести его к общему виду и построить прямую:
3.1 Прямая 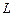 задана точкой
задана точкой 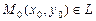 и нормальным вектором
и нормальным вектором 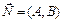 :
:
а) 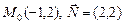 ; б)
; б) 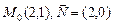 ; в)
; в) 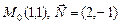 .
.
3.2 Прямая 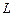 задана точкой
задана точкой 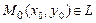 и направляющим вектором
и направляющим вектором 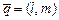 :
:
а) 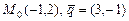 ; б)
; б) 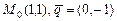 ; в)
; в) 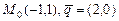 .
.
3.3 Прямая 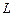 задана двумя своими точками
задана двумя своими точками 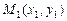 и
и 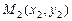 :
:
а) 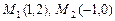 ; б)
; б) 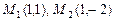 ; в)
; в) 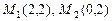 .
.
3.4 Определить угловой коэффициент и отрезки, отсекаемые на осях координат прямой, заданной уравнением. Построить прямую. 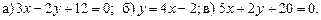
3.5 Вычислить угол между двумя прямыми: 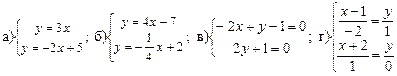 .
.
3.6 Через точку 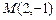 провести прямую, параллельную прямой
провести прямую, параллельную прямой 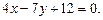
3.7 Написать уравнение перпендикуляра, опущенного из точки 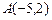 на прямую
на прямую 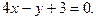
3.8 Написать уравнение прямой, которая проходит через начало координат и:
а) параллельна прямой 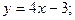 б) образует угол в
б) образует угол в 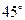 с прямой
с прямой 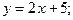
в) перпендикулярна 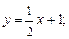 г) образует угол в
г) образует угол в 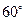 с прямой
с прямой 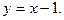
3.9 Через точку 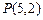 провести прямую, отсекающую равные отрезки на осях координат.
провести прямую, отсекающую равные отрезки на осях координат.
3.10 Написать уравнение прямой, которая проходит через точку 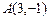 и параллельна: а) оси абсцисс; б) биссектрисе координатного угла; в) прямой
и параллельна: а) оси абсцисс; б) биссектрисе координатного угла; в) прямой 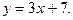
3.11 Даны вершины треугольника: 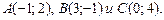 Через каждую из них провести прямую, параллельную противолежащей стороне.
Через каждую из них провести прямую, параллельную противолежащей стороне.
3. 12 Даны вершины треугольника: 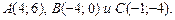 Составить уравнения:
Составить уравнения:
а) трех его сторон; б) высоты, опущенной из вершины 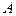 на сторону
на сторону 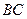 ;
;
в) медианы, проведенной из вершины 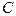 ; г) биссектрисы угла
; г) биссектрисы угла 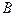 .
.
3.13 Определить площадь треугольника, заключенного между осями координат и прямой 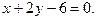
3.14 Через точку 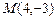 провести прямую так, чтобы площадь треугольника, образованного ею и осями, была равна
провести прямую так, чтобы площадь треугольника, образованного ею и осями, была равна 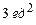 .
.
3.15 Найти расстояние точки 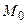 : а)
: а) 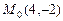 от прямой
от прямой 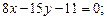
б) 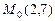 от прямой
от прямой 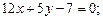 в)
в) 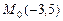 от прямой
от прямой 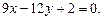
3.16 На оси ординат прямоугольной системы координат найти точку, одинаково удаленную от начала координат и от прямой 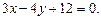
3.17 Доказать, что прямые 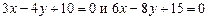 параллельны между собой, и найти расстояние между ними.
параллельны между собой, и найти расстояние между ними.
3.18 Даны уравнения двух параллельных прямых: 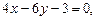
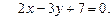 Составить уравнение прямой им параллельной и проходящей посередине между ними.
Составить уравнение прямой им параллельной и проходящей посередине между ними.
3.19 Найти точку, симметричную с точкой 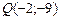 относительно прямой
относительно прямой 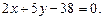
3.21 Даны уравнения сторон треугольника: 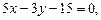
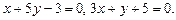 Вычислить координаты его вершин.
Вычислить координаты его вершин.
3.22 Даны две вершины треугольника 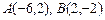 и точка
и точка 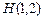 пересечения его высот. Вычислить координаты третьей вершины
пересечения его высот. Вычислить координаты третьей вершины 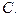
3.23 Составить уравнения высот треугольника, зная уравнения его сторон: 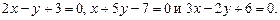
3.24 Составить уравнения сторон треугольника, зная одну из его вершин 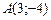 и уравнения двух высот:
и уравнения двух высот: 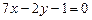 и
и 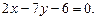
3.25 Составить уравнения сторон треугольника, зная одну из его вершин 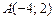 и уравнения двух медиан:
и уравнения двух медиан: 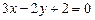 и
и 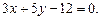
Ответы: 3.1 а) 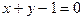 б)
б) 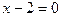 в)
в) 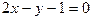 3.2 а)
3.2 а) 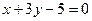 б)
б) 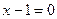 в)
в) 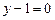 3.3 а)
3.3 а) 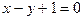 б)
б) 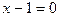 в)
в) 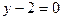 3.4 а)
3.4 а)  б)
б) 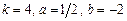 в)
в) 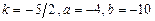 3.5 а)
3.5 а) 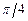 , б)
, б) 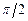 , в)
, в) 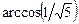 , г)
, г) 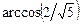 . 3.6
. 3.6 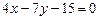 3.7
3.7 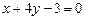 3.8 а)
3.8 а) 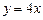 , б)
, б) 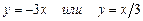 , в)
, в) 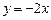 , г)
, г) 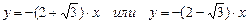 . 3.9
. 3.9 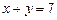 . 3.10 а)
. 3.10 а) 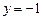 , б)
, б) 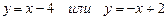 , в)
, в) 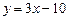 . 3.11
. 3.11 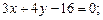
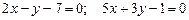 . 3.12 а)
. 3.12 а) 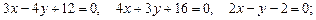 б)
б) 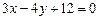 ; в)
; в) 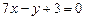 ; г)
; г) 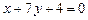 . 3.13 S=9. 3.14
. 3.13 S=9. 3.14 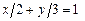 ;
; 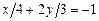 3.15
3.15 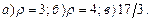 3.16
3.16 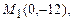
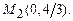 3.17
3.17 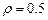 3.18
3.18 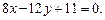 3.19
3.19 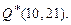 3.21 (3,0),
3.21 (3,0), 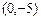 и
и 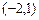 3.22
3.22 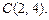 3.23
3.23 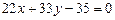 ,
, 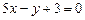 ,
, 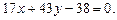 3.24
3.24 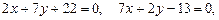
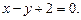 3.25
3.25 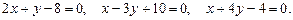
 2015-06-28
2015-06-28 1229
1229