2015-06-28
978
Рассмотрим какую-нибудь прямую p, пересекающую ось Ox; точку пересечения обозначим А. Возьмем на оси Ox точку В, лежащую правее А, а на прямой p точку С, лежащую в верхней полуплоскости. Угол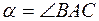 
называется углом наклона прямой p к оси Ox. Если же p||Ox, будем считать 
.
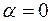Угловым коэффициентом прямой называют тангенс угла наклона ее к оси Ox; обозначение k: k= tg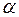 
. Так как всегда 0 ≤ 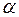< 180o, то угловой коэффициент, как и сам угол 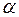, однозначно определяет наклон прямой к оси абсцисс.
Составим уравнение прямой p, проходящей через точку M 0(x 0, y 0) и имеющей угловой коэффициент k. Пусть M (x, y) – текущая точка прямой.
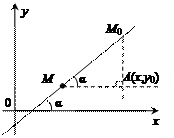
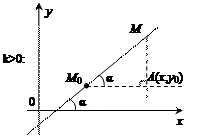
В зависимости от знака k и взаимного расположения точек М и М 0 возможны четыре случая:
 | |||||||
 | |||||||
 |  |
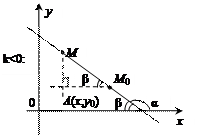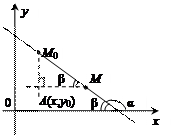Рассмотрим прямоугольный треугольник АМ 0 М и найдем тангенс
угла 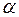(для первых двух случаев) и угла 
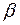(для двух других):
; 
;
; 
.
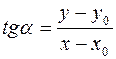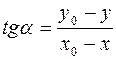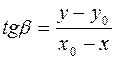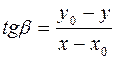Учитывая, что β= 180o –α, а значит 
все эти четыре формулы сводятся к одной
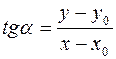. (1)
Но по определению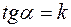 
, значит, (1) можно переписать в виде
у–y 0 =k (x–x 0). (2)
Это и есть искомое уравнение прямой, проходящей через точку M 0(x 0, y 0)и имеющую данный угловой коэффициент k.
Замечание 1. Уравнению (2) можно придать другую форму. Если положить b=y 0 –kx 0, то из (2) получим
y=kx+b. (3)
Этот вид записи уравнения прямой употребляется, пожалуй, наиболее часто. Его называют уравнением прямой с угловым коэффициентом. Свободный член b имеет простой геометрический смысл – это ордината точки пересечения прямой с осью Оу.
Замечание 2. Соотношение (1) справедливо для любой пары точек M (x, y) и M 0(x 0, y 0) прямой с углом наклона α. Используя этот факт, можно решить следующую задачу:
составить уравнение прямой, проходящей через две данные точки M 1(x 1, y 1) и M 2(x 2, y 2).
Для ее решения берем, как обычно, текущую точку M (x, y) и применяем соотношение (1) к двум парам точек: (M, М 1)и (M 2, М 1). Получим:
, 
.
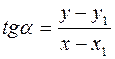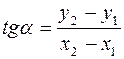Левые части этих равенств равны, следовательно, можно приравнять правые, а затем, используя свойство пропорции, записать уравнение
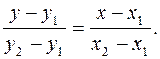(4)
Это и есть искомое уравнение прямой, проходящей через две данные точки M 1(x 1, y 1) и M 2(x 2, y 2).
Отметим, что к уравнению (4) можно прийти и другими способами.
Пример. Даны вершины треугольника A (2;–1), B (–1;–1) и C (3;2). Составить уравнение медианы, проведенной из вершины А.
Решение. Медиана треугольника соединяет его вершину А с серединой противоположной стороны ВС. Обозначим эту середину D (x 1, y 1) и найдем ее:
.
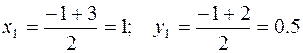Напишем теперь уравнение медианы, как прямой проходящей через две точки А (2;1)и D (1;0,5):
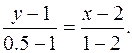
Упрощая, получим x– 2 y= 0, или y= 0.5 x.
Замечание 3. Между общим уравнением прямой и уравнением прямой с угловым коэффициентом существуют очевидные связи:
1) угловой коэффициент прямой Ax+By+C= 0имеет вид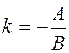 
(если только В ≠0, т.е. прямая не параллельна оси Oy);
2)нормальный вектор прямой у=kx+b имеет вид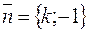 
(с точ- ностью до коллинеарности).
