Общее уравнение прямой на плоскости

Будем считать, что на плоскости задана некоторая ДПСК.

Определение. Всякий ненулевой вектор, перпендикулярный данной прямой, называется её нормальным вектором. Стандартное обозначение: .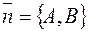

Очевидно, что всякая прямая имеет бесконечно много нормальных векторов, но все они коллинеарны друг другу.

Теорема. В декартовых координатах всякая прямая определяется уравнением первой степени, т.е. уравнением вида

Ax+By+C= 0. (1)

И обратно: всякое уравнение вида (1) определяет на плоскости некоторую прямую.

Доказательство. Докажем прямую часть теоремы. Пусть на плоскости задана прямая p и пусть точка M ₀(x ₀, y ₀) – некоторая принадлежащая ей точка, а 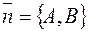– её нормальный вектор. Как обычно

при выводе уравнений, берем текущую точку прямой M (x, y) и рассматриваем вектор 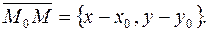Тогда:

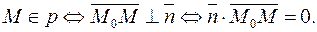
Выражая скалярное произведение векторов через их проекции, получаем:

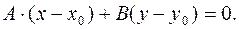(2)

Это и есть искомое уравнение прямой. Раскрыв скобки, его нетрудно записать в форме (1):

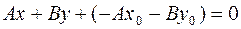и обозначив ,

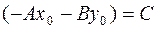получим уравнение (1).

Докажем обратную часть теоремы. Пусть дано произвольное уравнение вида (1). Термин “произвольное” означает, что коэффициенты A, B, C могут быть какими угодно числами, исключая, конечно, случай одновременного равенства A=B= 0. Мы должны доказать, что такое уравнение определяет некоторую прямую.

Пусть x ₀, y ₀ – какое-нибудь решение уравнения (1) (например, x ₀ – произвольное, а y ₀ = (–C–Ax ₀) /B, если В≠ 0; если же В= 0, то y ₀ – произвольное, а 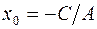). Это означает, что

Ax ₀ +By ₀ +C= 0 – (3)

верное числовое равенство. Вычтем из уравнения (1) равенство (3). Получим

уравнение

A (x–x ₀) +B (y–y ₀) = 0, (2)

равносильное исходному уравнению (1). Но согласно уже доказанному, такое уравнение имеет прямая проходящая через точку с координатами x ₀ и y₀, для которой 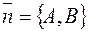– нормальный вектор. Теорема доказана.

Замечание 1. Уравнение

Ax+By+C= 0 (1)

называют общим уравнением прямой. Уравнение же

A (x–x ₀) +B (y–y ₀) = 0 (2)

есть уравнение прямой, проходящей через точку M ₀(x ₀; y ₀) и имеющей нормальный вектор .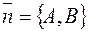

Пример. Даны вершины треугольника A (2;1), B (–1;–1) и C (3;2). Составить уравнение высоты AD, опущенной из вершины А на сторону ВС.

Решение. Для высоты AD вектор 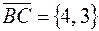является нормальным. Поэтому, используя (2), можно написать искомое уравнение:

4(x– 2) + 3(y– 1) = 0,

или 4 x+ 3 y– 11 = 0.

Замечание 2. В случае, когда один или два из коэффициентов уравнения (1) равны 0, уравнение называют неполным. Неполные уравнения определяют на плоскости характерные прямые.

1) С= 0; уравнение Ax+By= 0 определяет прямую, проходящую через начало координат.

2) В= 0(А≠ 0) означает: 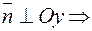прямая параллельна оси Oy.