2015-06-28
593
В этом параграфе мы приведем условия параллельности и перпендикулярности прямых, а также формулы, позволяющие найти угол между прямыми.
Пусть даны две прямые
p 1: A 1 x+B 1 y+C 1 = 0, p 1: y=k 1 x+b 1,
p 2: A 2 x+B 2 y+C 2 = 0, p 2: y=k 2 x+b 2.
1. Прямые параллельны тогда и только тогда, когда их нормальные векторы коллинеарные, или угловые коэффициенты равны:
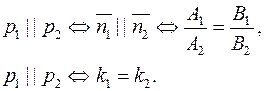
2. Прямые перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны:
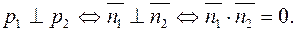
Это в терминах проекций означает следующее:
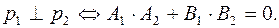
Если же прямые заданы в форме уравнений с угловыми коэффициентами, то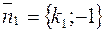 
и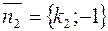 
и условие перпендикулярности принимает вид:
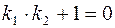или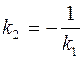 
.
3. Один из двух углов, которые образуют две пересекающиеся прямые (их сумма равна π), равен углу между нормальными векторами этих прямых, и его косинус может быть найден по известной формуле. Если же мы хотим находить острый угол φ между прямыми, эта формула модифицируется:
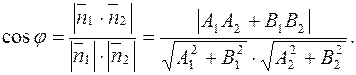
В случае задания прямых в форме уравнений с угловыми коэффициентами можно пользоваться и другой формулой:
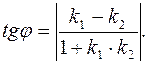
Пример. Дана прямая p: y= 2 x+ 3 и точка M 0(1;2). Через точку M 0 провести: 1)прямую q 1 ||p; 2) прямую q 2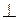 
p.
Решение. Зная угловой коэффициент прямой p,а именно: k= 2, нетрудно найти угловые коэффициенты прямых q 1 и q 2. Имеем:
k 1 =k= 2, k 2 =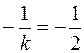 
.
После этого находим искомые уравнения, как уравнения прямых, проходящих через данную точку и имеющих данные угловые коэффициенты:
q 1: y– 2=2(x– 1),или y= 2 x;
q 2: y– 2 =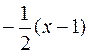 
,или y= – 0.5 x+ 2.5.
ЛЕКЦИЯ 7
