2015-06-28
331
Доказательство прямых теорем.
Пусть даны две прямые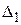 
и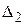 
, в некоторой системе координат их можно задать уравнениями 
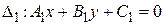с направляющим вектором 
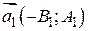и 
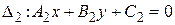с направляющим вектором 
.
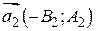1) Рассмотрим систему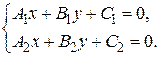 
Система имеет единственное решение, тогда и только тогда, когда 
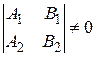, т.е. 
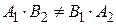или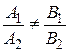 
.
2) 
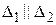, следовательно, 
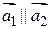, откуда 
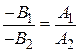. Рассмотрим систему 
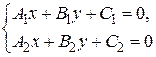. Умножим второе уравнение системы на 
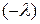и сложим с первым. Получаем систему вида 
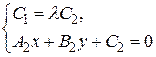. Последняя система не имеет решения, если 
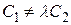. Т.е. получаем 
.
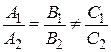3) Т.к.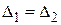 
, следовательно 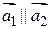, если 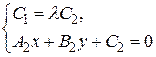– система имеет бесконечно много решений, если 
.
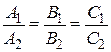Доказательство обратных теорем.
Пусть даны две прямые 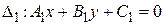и 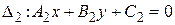. Рассмотрим систему 
.
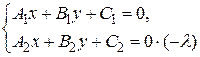1) если система имеет единственное решение, ,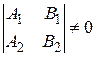 
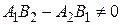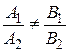, , откуда 
.
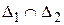2) Если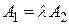 
, 
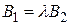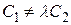, . Система примет вид 
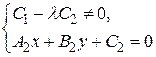– первое уравнение не имеет решений, значит вся система не имеет решений, следовательно .
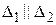3) Если , ,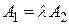 
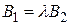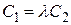. Система примет вид 
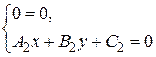– система имеет бесконечно много решений.
Теорема доказана.
Если прямые пересекаются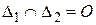 
, Запишем систему 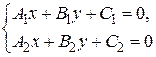. Координаты точки пересечения прямых можно найти по формулам
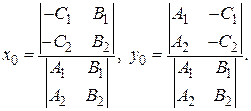(3.1)
