Пример 3.1. Определите взаимное расположение прямых.
a) 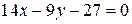 и
и 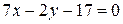 ;
;
b) 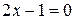 и
и 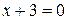 ;
;
c) 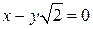 и
и 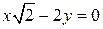 .
.
Решение.
a) 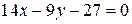 и
и 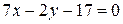 . Рассмотрим отношение коэффициентов:
. Рассмотрим отношение коэффициентов: 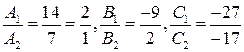 . В соответствии с доказанной теоремой имеем случай
. В соответствии с доказанной теоремой имеем случай 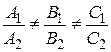 , т.е. прямые пересекаются.
, т.е. прямые пересекаются.
b) 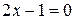 и
и 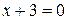 . Рассмотрим отношение коэффициентов:
. Рассмотрим отношение коэффициентов: 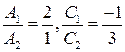 , для отношения коэффициентов
, для отношения коэффициентов 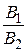 возможны любые случаи. В соответствии с доказанной теоремой имеем случай
возможны любые случаи. В соответствии с доказанной теоремой имеем случай 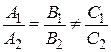 , т.е. прямые параллельны.
, т.е. прямые параллельны.
c) 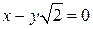 и
и 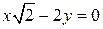 . Рассмотрим отношение коэффициентов:
. Рассмотрим отношение коэффициентов: 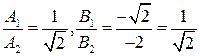 , для отношения коэффициентов
, для отношения коэффициентов 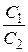 возможны любые случаи. В соответствии с доказанной теоремой имеем случай
возможны любые случаи. В соответствии с доказанной теоремой имеем случай 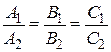 , т.е. прямые совпадают.
, т.е. прямые совпадают.
Ответ.
a) Прямые 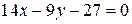 и
и 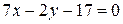 пересекаются.
пересекаются.
b) Прямые 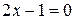 и
и 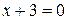 параллельны.
параллельны.
c) Прямые 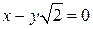 и
и 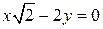 совпадают.
совпадают.
Пример3.2. Доказать, что прямые 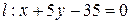 и
и 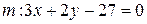 пересекаются и найти точку их пересечения.
пересекаются и найти точку их пересечения.
Решение. Рассмотрим отношение коэффициентов: 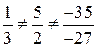 . В соответствии с доказанной теоремой имеем случай
. В соответствии с доказанной теоремой имеем случай 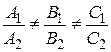 , т.е. прямые пересекаются.
, т.е. прямые пересекаются.
Точку пересечения определим по формулам (3.1):
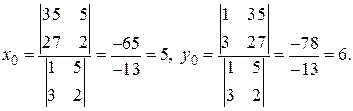
Т.е. 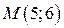 – точка пересечения прямых
– точка пересечения прямых 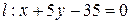 и
и 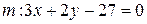 .
.
Ответ. 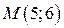 .
.
 2015-06-28
2015-06-28 369
369








