Блок теоретических материалов «Частные случаи расположения прямой на плоскости относительно системы координат»
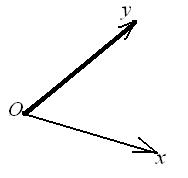
Пусть 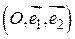 – аффинный репер,
– аффинный репер, 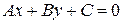 – уравнение некоторой прямой, где
– уравнение некоторой прямой, где 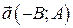 – направляющий вектор.
– направляющий вектор.
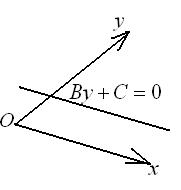 1) Если
1) Если 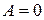 , тогда
, тогда 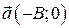 , следовательно, уравнение прямой примет вид
, следовательно, уравнение прямой примет вид 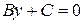 . Откуда
. Откуда 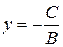 . Следовательно, прямая параллельна оси
. Следовательно, прямая параллельна оси 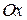 .
.
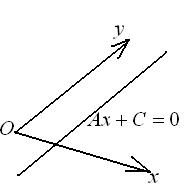
2) Если 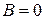 , тогда
, тогда 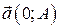 , следовательно, уравнение прямой примет вид
, следовательно, уравнение прямой примет вид 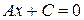 . Откуда
. Откуда 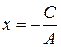 . Следовательно, прямая параллельна оси
. Следовательно, прямая параллельна оси 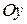 .
.
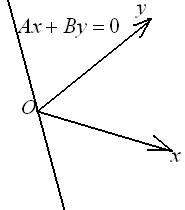
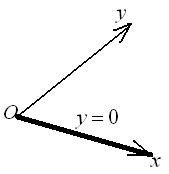
3) 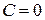 , следовательно, уравнение прямой примет вид
, следовательно, уравнение прямой примет вид 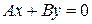 .
. 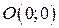 , тогда
, тогда 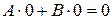 – верно. Значит,
– верно. Значит, 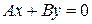 проходит через точку
проходит через точку 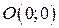 .
.
4) 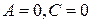 , следовательно, уравнение прямой примет вид
, следовательно, уравнение прямой примет вид 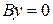 или
или 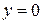 – уравнение оси
– уравнение оси 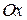 .
.
5) 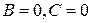 , следовательно, уравнение прямой примет вид
, следовательно, уравнение прямой примет вид 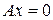 или
или 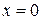 – уравнение оси
– уравнение оси 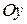 .
.
Пример 2.1. Определите расположение прямых относительно системы координат
a) 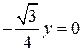 ;
;
b) 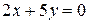 ;
;
c) 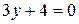 ;
;
d) 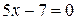 ;
;
e) 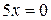 .
.
Решение.
Из ранее изученного вами материала известно, что общим уравнением прямой называется прямая в виде 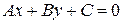 .
.
a) 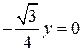 . Заданное уравнение можно переписать в виде
. Заданное уравнение можно переписать в виде 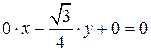 . Следовательно
. Следовательно 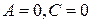 , откуда, в соответствии с пунктом 4) получаем, что прямая
, откуда, в соответствии с пунктом 4) получаем, что прямая 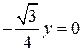 совпадает с осью
совпадает с осью 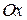 .
.
b) 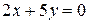 . Заданное уравнение можно переписать в виде
. Заданное уравнение можно переписать в виде 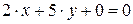 . Следовательно
. Следовательно 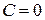 , откуда, в соответствии с пунктом 3) получаем, что прямая
, откуда, в соответствии с пунктом 3) получаем, что прямая 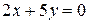 проходит через начало координат.
проходит через начало координат.
c) 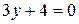 . Заданное уравнение можно переписать в виде
. Заданное уравнение можно переписать в виде 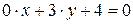 . Следовательно
. Следовательно 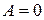 , откуда, в соответствии с пунктом 1) получаем, что прямая
, откуда, в соответствии с пунктом 1) получаем, что прямая 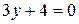 параллельна оси
параллельна оси 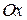 .
.
d) 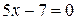 . Заданное уравнение можно переписать в виде
. Заданное уравнение можно переписать в виде 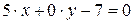 . Следовательно
. Следовательно 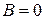 , откуда, в соответствии с пунктом 3) получаем, что прямая
, откуда, в соответствии с пунктом 3) получаем, что прямая 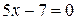 параллельна оси
параллельна оси 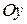 .
.
e) 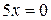 . Заданное уравнение можно переписать в виде
. Заданное уравнение можно переписать в виде 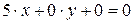 . Следовательно
. Следовательно 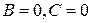 , откуда, в соответствии с пунктом 5) получаем, что прямая
, откуда, в соответствии с пунктом 5) получаем, что прямая 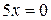 совпадает с осью
совпадает с осью 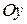 .
.
Ответ. а) Прямая, заданная уравнением 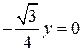 совпадает с осью
совпадает с осью 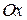 .
.
b) Прямая, заданная уравнением 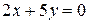 проходит через начало координат.
проходит через начало координат.
c) Прямая, заданная уравнением 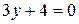 параллельна оси
параллельна оси 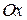 .
.
d) Прямая, заданная уравнением 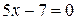 параллельна оси
параллельна оси 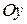 .
.
e) Прямая, заданная уравнением 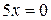 совпадает с осью
совпадает с осью 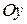 .
.
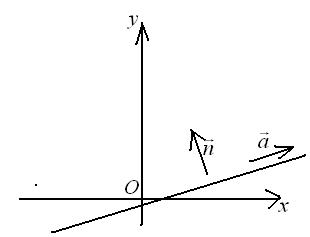
Рассмотрим прямоугольную систему координат 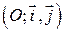 и прямую
и прямую 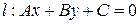 .
. 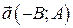 – направляющий вектор прямой,
– направляющий вектор прямой, 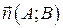 – главный вектор прямой.
– главный вектор прямой.
Докажем, что вектор 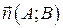 является нормальным вектором к прямой
является нормальным вектором к прямой 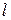 . Для этого найдем скалярное произведение
. Для этого найдем скалярное произведение 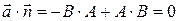 . Откуда получаем
. Откуда получаем 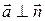 .
. 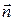 – нормальный вектор прямой
– нормальный вектор прямой 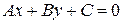 .
.
Пример 2.2. Докажите, что вектор 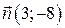 является нормальным вектором прямой
является нормальным вектором прямой 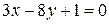 .
.
Доказательство. Пусть заданный вектор 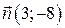 является нормальным вектором прямой
является нормальным вектором прямой 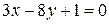 . Из задания уравнения прямой имеем
. Из задания уравнения прямой имеем 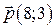 – ее направляющий вектор. Если вектор
– ее направляющий вектор. Если вектор 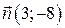 является нормальным вектором заданной прямой, то скалярное произведение
является нормальным вектором заданной прямой, то скалярное произведение 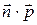 должно ровняться нулю. Проверим это,
должно ровняться нулю. Проверим это,
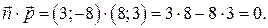
 2015-06-28
2015-06-28 460
460








