Блок теоретических материалов «Расстояние от точки до прямой»
Пусть 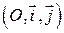 – прямоугольная система координат. Необходимо определить расстояние от точки
– прямоугольная система координат. Необходимо определить расстояние от точки 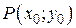 до прямой
до прямой 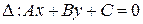 .
.
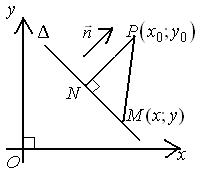 Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из этой точки на прямую (если точка принадлежит прямой, то расстояние равно нулю).
Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из этой точки на прямую (если точка принадлежит прямой, то расстояние равно нулю).
Пусть 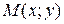 – произвольная точка прямой,
– произвольная точка прямой, 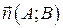 – нормальный вектор,
– нормальный вектор, 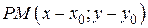 .
.
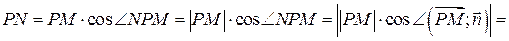
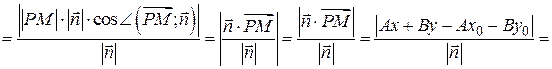
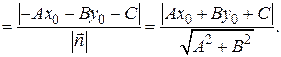
Таким образом,
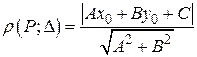 . (4.1)
. (4.1)
Пример 4.1. Найти расстояние от точки 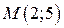 до прямой
до прямой 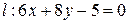 .
.
Решение. Воспользуемся формулой (4.1):
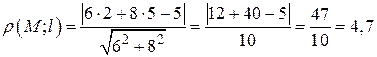 .
.
Ответ. 4,7.
Пример 4.2. Найти расстояние между двумя параллельными прямыми 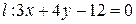 и
и 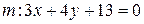 .
.
Решение. Искомое расстояние найдем как расстояние от произвольной точки первой прямой до второй прямой. Возьмем на первой прямой произвольную точку, например, точку с абсциссой 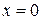 . Ее ордината будет
. Ее ордината будет  .
.
Итак, на первой прямой выбрана точка 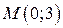 . Найдем теперь расстояние от этой точки до второй прямой по формуле (4.1):
. Найдем теперь расстояние от этой точки до второй прямой по формуле (4.1):
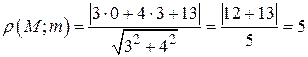 .
.
Ответ. 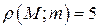 .
.
Пример 4.3. Дана прямая 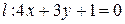 . Найти уравнение прямой, параллельной данной и находящейся от нее расстоянии 3.
. Найти уравнение прямой, параллельной данной и находящейся от нее расстоянии 3.
Решение. Так как искомых прямых будет 2 (они расположены по две стороны от данной прямой на расстоянии 3).
Уравнение семейства прямых, параллельных данной, будет следующим:
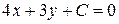 .
.
Пусть 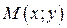 произвольная точка прямой
произвольная точка прямой 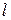 . Определим искомые прямые, воспользовавшись формулой (4.1):
. Определим искомые прямые, воспользовавшись формулой (4.1):
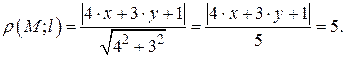
При раскрытии модуля получаем 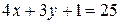 или
или 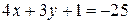 . После приведения подобных получаем
. После приведения подобных получаем 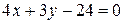 или
или 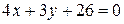 .
.
Ответ: 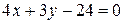 или
или 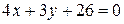 .
.
 2015-06-28
2015-06-28 295
295








