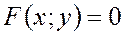 (1)
(1)
Определение. Пусть на плоскости рассматривается линия L: уравнение (1) называется уравнением линии L, если любая точка на линии L имеет координаты в данной системе координат, которые удовлетворяют уравнению (1). И любая точка, не лежащая на линии L, имеет координаты, неудовлетворяющие уравнению (1).
Определение. Многочленом степени n от двух переменных (x и y) называется сумма, каждое слагаемое которой представляет произведение вида 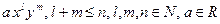 , при этом имеется хотя бы одно слагаемое, удовлетворяющее
, при этом имеется хотя бы одно слагаемое, удовлетворяющее 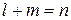 .
.
Определение. Уравнение (1), в котором функция представляет собой многочлен степени n от двух переменных, называется алгебраическим уравнением степени n.
Определение. Линии плоскости, описываемые алгебраическими уравнениям степени n, называются алгебраическими линиями n-го порядка.
Пример:
1. 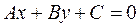
2. 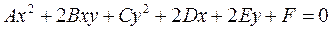
 2015-06-28
2015-06-28 330
330








