Лемма
Степень уравнения линии не зависит от выбора системы координат.
Теорема 1
Любое уравнение первой степени от двух неизвестных описывает прямую линию на плоскости. Любая прямая линия на плоскости описывается уравнением первой степени.
Д-во:
1. 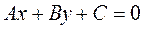 (2).
(2).
Докажем, что это уравнение прямой линии.
Пусть 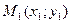 ,
, 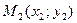 ,
, 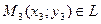 ,
,
L – линия, описывающая (2).
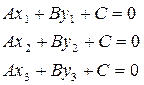
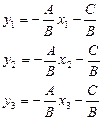
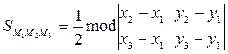
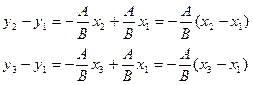
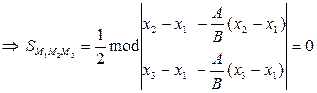
Следовательно, три точки 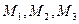 лежат на одной прямой. Ввиду произвольности этих точек сделаем вывод, что (2) – уравнение прямой.
лежат на одной прямой. Ввиду произвольности этих точек сделаем вывод, что (2) – уравнение прямой.
2. Пусть L – прямая на плоскости. Пусть L совпадает с осью 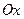 в выбранной системе координат:
в выбранной системе координат: 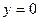 по определению. Это уравнение первой степени. По лемме наша прямая описывается уравнением первой степени в любой другой системе координат.
по определению. Это уравнение первой степени. По лемме наша прямая описывается уравнением первой степени в любой другой системе координат.
Теорема доказана
Уравнение (2) называется общим уравнением прямой. Пусть 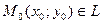 с уравнением (2)
с уравнением (2) 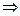
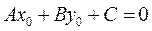 (*)
(*)
(2)-(*):
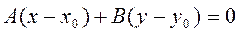 (3)
(3)
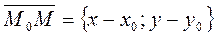 ,
, 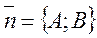
Пусть уравнение (2) рассматривается в прямоугольной декартовой системе координат (ПДСК) на плоскости, тогда условие (3) означает: 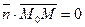
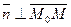
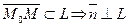
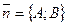 - нормальный вектор прямой с уравнением (2).
- нормальный вектор прямой с уравнением (2).
Уравнение (3) - уравнение прямой, проходящей через точку 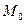 с данным нормальным вектором.
с данным нормальным вектором.
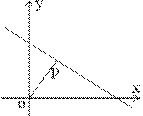
Задача
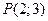 - основание перпендикуляра, опущенного из начала координат на прямую. Написать уравнение прямой
- основание перпендикуляра, опущенного из начала координат на прямую. Написать уравнение прямой
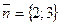
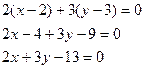
 2015-06-28
2015-06-28 411
411








