Неполное уравнение прямой. Уравнения в отрезках

Уравнение (2) называется полным, если 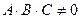, т.е. ни один из коэффициентов не равен нулю, иначе оно неполное.

Неполное уравнение прямой:

1.

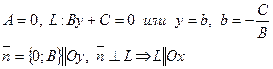
2.

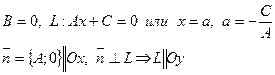
3. 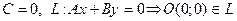(прямая проходит через начало координат).

4.

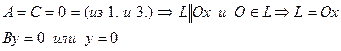
5.

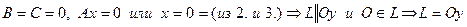
Полное уравнение прямой:

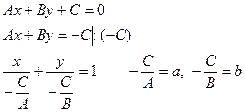
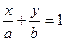(4)

Геометрический смысл коэффициентов a и b в уравнении (4)

Пересечем L с Ox, y=0.

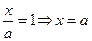, (a; 0) – точка пересечения L с Ox.

Пересечем L с Oy, x=0.

y=b (0; b) – точка пересечения L с Oy.

Уравнение (4) называется уравнением в отрезках, a и b – координаты концов этих отрезков.