Различные уравнения прямой на плоскости

1. Дано: 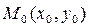в аффинной системе координат (АСК), 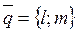в АСК.

Найти: уравнение прямой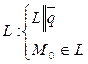

Решение:

Пусть 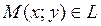- текущая точка на L.

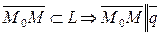
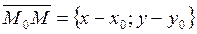
Условие коллинеарности: пропорциональность соответствующих координат. 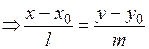(8)

(8) называется каноническим уравнением прямой, 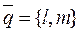- направляющий вектор прямой с уравнением (8).

Рассмотрим

Вектор 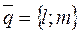заданный в ПДСК. Приложим 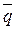к началу координат.

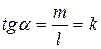- угловой коэффициент вектора 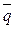(9)

2. Из школьного курса геометрии известно, что через любые две несовпадающие точки можно провести только одну прямую.

Дано: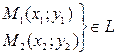

Найти: уравнение L

Решение:

Пусть 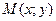- текущая точка на прямой L.

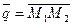и

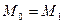
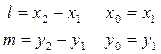
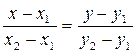(7)

Замечание: Деление на 0 понимается в смысле пропорции:

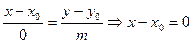
Рассмотрим каноническое уравнение (8)

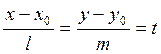
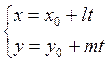(8) - параметрические уравнения прямой.

Выразим 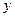из уравнения (5): 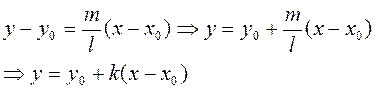(9)

α – угол наклона вектора 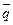и прямой L к оси Ox в уравнении (6) (изменяется в пределах [0; π]).

Уравнение (9) называется уравнением прямой с данным угловым коэффициентом, проходящей через данную точку.

Рассмотрим уравнение (9):

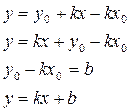(10)

(10)- уравнение прямой с угловым коэффициентом k (точка (0; b) – точка пересечения прямой с осью Oy).

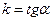- тангенс угла наклона прямой L к оси Ox.