Прямая на плоскости
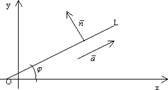 Уравнением линии называется уравнение с переменными x и y Ф(х,у) = 0, которому удовлетворяют координаты любой точки этой линии и только они.
Уравнением линии называется уравнение с переменными x и y Ф(х,у) = 0, которому удовлетворяют координаты любой точки этой линии и только они.
Замечание. Часто удобно использовать параметрические уравнения линии: 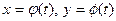 , где функции
, где функции 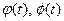 непрерывны по параметру t.
непрерывны по параметру t.
1) Общее уравнение прямой на плоскости имеет вид
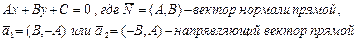 .
.
2) Частные случаи
| Значение коэффициента | Вид уравнения | Положение прямой |
| С=0 | Ax+By=0 y=kx | проходит через начало координат |
| A=0 | By+C=0 y=b | параллельна оси Ox |
| B=0 | Ax+C=0 x=a | параллельна оси Oy |
| A=C=0 | y=0 | совпадает с осью Ox |
| B=C=0 | x=0 | совпадает с осью Oy |
3) Векторное уравнение
Пусть М0(х0,у0) – заданная точка прямой, 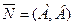 - ненулевой вектор, перпендикулярный прямой (он называется нормальным вектором прямой). Тогда векторное уравнение прямой имеет вид
- ненулевой вектор, перпендикулярный прямой (он называется нормальным вектором прямой). Тогда векторное уравнение прямой имеет вид
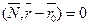 ,
,
где М(х,у) – произвольная точка на прямой и вектор 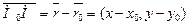 - вектор, перпендикулярный вектору нормали. Если переписать уравнение в координатной форме, то получим
- вектор, перпендикулярный вектору нормали. Если переписать уравнение в координатной форме, то получим
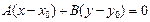
4) Уравнение прямой в «отрезках»
Если 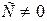 , то после преобразования общего уравнения имеем
, то после преобразования общего уравнения имеем
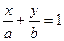 ,
,
где a и b – соответственно абсцисса и ордината точек пересечения прямой с осями Ox и Oy.
5) Уравнение прямой с угловым коэффициентом
Если 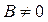 , то после преобразования общего уравнения имеем
, то после преобразования общего уравнения имеем
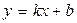 ,
,
где 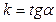 - угловой коэффициент, b – начальная ордината.
- угловой коэффициент, b – начальная ордината.
6) Уравнение прямой, проходящей через две точки
Пусть прямая проходит через две точки А(х1,у1) и В(х2,у2). Тогда ее уравнение
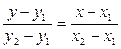 ,
,
где 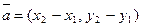 - направляющий вектор данной прямой.
- направляющий вектор данной прямой.
7) Канонические уравнения прямой
Пусть М(х0,у0) – заданная точка прямой, а 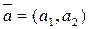 - направляющий вектор прямой. Тогда канонические уравнения прямой на плоскости имеют вид
- направляющий вектор прямой. Тогда канонические уравнения прямой на плоскости имеют вид
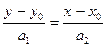 .
.
8) Параметрические уравнения прямой
Рассмотрим канонические уравнения прямой и введем параметр t
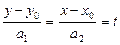 . Тогда получим систему, которая дает параметрические уравнения прямой на плоскости
. Тогда получим систему, которая дает параметрические уравнения прямой на плоскости
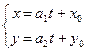
9) Уравнение прямой, проходящей через точку в заданном направлении
Уравнение прямой, проходящей через точку А(х1,у1) под углом φ к положительному направлению оси Ох, имеет вид 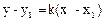 , где k=tgφ – угловой коэффициент прямой.
, где k=tgφ – угловой коэффициент прямой.
10) Угол между двумя прямыми
Если прямые заданы общими уравнениями 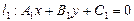 и
и 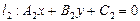 , то
, то
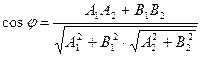 .
.
Угол φ между прямыми с угловыми коэффициентами k1 и k2 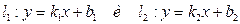 определяется из соотношения
определяется из соотношения
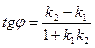 .
.
Угол φ между прямыми, заданными каноническими уравнениями 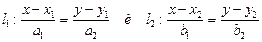 определяется из соотношения
определяется из соотношения
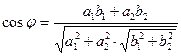 .
.
Данные формулы определяют значение тригонометрической функции одного из двух углов (острого или тупого) между заданными прямыми. Для нахождения острого угла между прямыми выражения в правой части этих формул следует брать по модулю.
11) Условие параллельности прямых
Если прямые заданы общими уравнениями 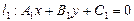 и
и 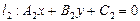 , то они параллельны в случае
, то они параллельны в случае 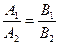 .
.
Если прямые заданы уравнениями с угловыми коэффициентами 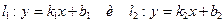 , то они параллельны в случае k1= k2.
, то они параллельны в случае k1= k2.
Если прямые заданы каноническими уравнениями 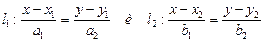 , то они параллельны в случае
, то они параллельны в случае 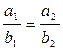 .
.
12) Условие перпендикулярности прямых
Если прямые заданы общими уравнениями 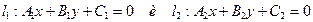 , то они перпендикулярны в случае
, то они перпендикулярны в случае 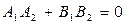 .
.
Если прямые заданы уравнениями с угловыми коэффициентами 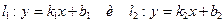 , то они перпендикулярны в случае k1= - 1/k2.
, то они перпендикулярны в случае k1= - 1/k2.
Если прямые заданы каноническими уравнениями 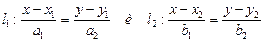 , то они перпендикулярны в случае
, то они перпендикулярны в случае 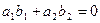 .
.
13) Деление отрезка в заданном соотношении
Если точка (х,у) делит отрезок, ограниченный точками А(х1,у1) и В(х2,у2) в отношении λ, то ее координаты определяются
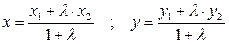 .
.
Координаты точки С, делящей отрезок АВ пополам
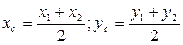 .
.
14) Расстояние между точками
Расстояние dAB между точками А(х1,у1) и В(х2,у2):
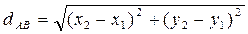 .
.
15) Расстояние от точки до прямой
Расстояние d от заданной точки М0(х0,у0) до заданной прямой с уравнением Ах+Ву+С=0 определяется по формуле
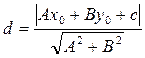 .
.
 2015-06-28
2015-06-28 326
326







