Прямая на плоскости.
Уравнение прямой на плоскости может быть задано:
1) с помощью углового коэффициента и «отрезка», отсекаемого от координатной оси 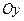 ;
;
2) точкой, лежащей на прямой, и вектором, параллельным прямой (направляющим вектором);
3) двумя точками;
4) точкой прямой и вектором, перпендикулярным прямой (нормальным вектором);
5) в «отрезках»;
6) ортом нормального вектора и расстоянием от начала координат до прямой.
1) Как известно, 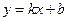 - уравнение прямой, которая проходит через точку
- уравнение прямой, которая проходит через точку 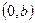 и составляет с положительным направлением оси
и составляет с положительным направлением оси 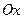 угол, тангенс которого равен
угол, тангенс которого равен 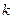 . Если указанная прямая проходит через точку
. Если указанная прямая проходит через точку 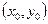 , то
, то  и вычитая полученное тождество из уравнения прямой, имеем
и вычитая полученное тождество из уравнения прямой, имеем 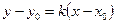 . Это уравнение прямой, проходящей через точку
. Это уравнение прямой, проходящей через точку 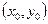 , с угловым коэффициентом
, с угловым коэффициентом 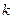 .
.
Если прямые 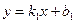 ,
, 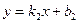 параллельны, то их угловые коэффициенты совпадают.
параллельны, то их угловые коэффициенты совпадают.
Если прямые 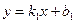 ,
, 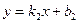 перпендикулярны, то
перпендикулярны, то 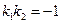 .
.
2) Пусть 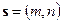 - направляющий вектор прямой, проходящей через точку
- направляющий вектор прямой, проходящей через точку 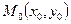 .
.
Для любой точки 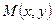 , лежащей на этой прямой, вектор
, лежащей на этой прямой, вектор 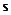 ||
|| 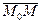 , поэтому
, поэтому 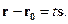
Определение. Уравнение 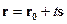 называется векторным уравнением прямой на плоскости (сравните с векторным уравнением прямой в пространстве).
называется векторным уравнением прямой на плоскости (сравните с векторным уравнением прямой в пространстве).
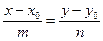 - каноническое уравнение прямой, проходящей через точку
- каноническое уравнение прямой, проходящей через точку 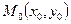 , с направляющим вектором
, с направляющим вектором 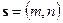 , векторное уравнение которой
, векторное уравнение которой 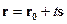 .
.
3) Если прямая задана двумя точками 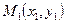 и
и 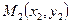 этой прямой, то
этой прямой, то 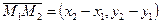 является направляющим вектором и
является направляющим вектором и 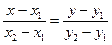 - уравнение прямой, проходящей через точки
- уравнение прямой, проходящей через точки 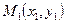 и
и 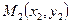 .
.
4) Пусть 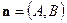 - нормальный вектор прямой, проходящей через точку
- нормальный вектор прямой, проходящей через точку 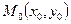 .
.
Для любой точки 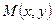 , лежащей на этой прямой, вектор
, лежащей на этой прямой, вектор 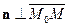 поэтому
поэтому 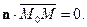
Определение. Уравнение
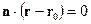
называется векторным уравнением прямой, заданной точкой и нормальным вектором прямой (сравните с векторным уравнением плоскости в пространстве).
Уравнение 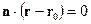 в координатной форме имеет вид
в координатной форме имеет вид
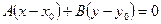 .
.
Если 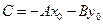 , то имеем уравнение
, то имеем уравнение 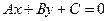 .
.
Определение. Уравнение 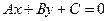 называется общим уравнением прямой на плоскости.
называется общим уравнением прямой на плоскости.
5) Определение. 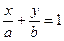 - уравнение прямой в «отрезках». Очевидно, прямая проходит через точки
- уравнение прямой в «отрезках». Очевидно, прямая проходит через точки 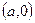 и
и 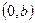 .
.
 6) Прямая может быть задана ортом нормального вектора
6) Прямая может быть задана ортом нормального вектора 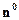 , направленного из начала координат в сторону прямой, и расстоянием от начала координат до этой прямой.
, направленного из начала координат в сторону прямой, и расстоянием от начала координат до этой прямой.
Пусть 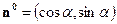 - орт нормального вектора прямой, а
- орт нормального вектора прямой, а 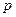 -
-
расстояние от начала координат до
Рис.3.26 прямой (рис.3.26).
Из начала координат опустим перпендикуляр на прямую. Точку пересечения перпендикуляра и прямой обозначим 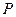 . Для любой точки прямой
. Для любой точки прямой 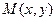 проекция вектора
проекция вектора 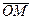 на направление вектора
на направление вектора 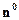 равна
равна 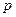 , т.е.
, т.е. 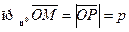 , откуда
, откуда 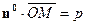 и
и 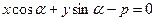 .
.
Определение. Уравнение 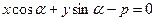 называется нормированным уравнением прямой.
называется нормированным уравнением прямой.
Общее уравнение прямой 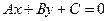 можно привести к нормированному виду
можно привести к нормированному виду 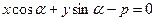 .
.
Определение. Число 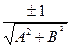 называется нормирующим множителем.
называется нормирующим множителем.
Умножив общее уравнение прямой на нормирующий множитель, взятый со знаком плюс, если 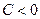 , и со знаком минус, если
, и со знаком минус, если 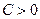 , получим нормированное уравнение прямой.
, получим нормированное уравнение прямой.
Замечание. Так как 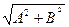 есть длина нормального вектора
есть длина нормального вектора 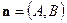 общего уравнения прямой, то нормирующий множитель равен
общего уравнения прямой, то нормирующий множитель равен 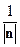 , если
, если 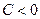 , и
, и 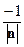 , если
, если 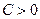 .
.
 2015-06-28
2015-06-28 1347
1347

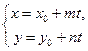 -
-