● Пример 28. Через точку пересечения прямых  и
и 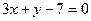 провести прямую,
провести прямую,
1) проходящую через начало координат;
2) проходящую через точку 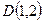 ;
;
3) параллельную оси 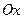 ;
;
4) параллельную оси 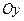 ;
;
5) параллельную прямой 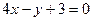 ;
;
6) перпендикулярную прямой 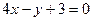 ;
;
7) отсекающую на осях координат равные отрезки.
Анализ задачи Уравнение пучка прямых, проходящих через точку пересечения прямых  и
и 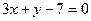 имеет вид
имеет вид 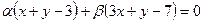 - или
- или
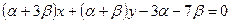 . (3.15)
. (3.15)
Вектор 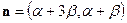 - нормальный вектор этого пучка прямых.
- нормальный вектор этого пучка прямых.
Из системы 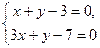 имеем
имеем 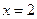 ,
, 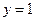 , т.е. точка
, т.е. точка 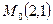 - точка пересечения данных прямых.
- точка пересечения данных прямых.
● Пример 28. Через точку пересечения прямых  и
и 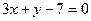 провести прямую,
провести прямую,
1) проходящую через начало координат;
1) Первый способ. Так как искомая прямая принадлежит пучку прямых и проходит через начало координат, то из 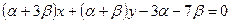 . (3.15)
. (3.15)
следует 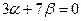 . Выбрав
. Выбрав 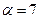 , получим
, получим 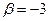 . Искомое уравнение имеет вид
. Искомое уравнение имеет вид 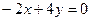 или
или 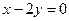 .
.
Второй способ. Так как искомая прямая проходит через начало координат, то уравнение этой прямой имеет вид 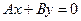 . Точка
. Точка 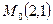 принадлежит этой прямой, поэтому
принадлежит этой прямой, поэтому 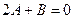 , откуда при
, откуда при 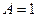 ,
, 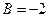 и
и 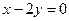 - уравнение искомой прямой.
- уравнение искомой прямой.
● Пример 28. Через точку пересечения прямых  и
и 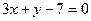 провести прямую,
провести прямую,
2) проходящую через точку 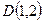 ;
;
2) Первый способ. Точка 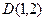 принадлежит пучку прямых, поэтому из
принадлежит пучку прямых, поэтому из 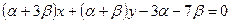 . (3.15)
. (3.15)
имеем 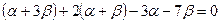 , откуда
, откуда 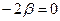 ,
, 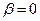 ,
, 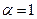 и
и 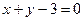 - уравнение искомой прямой.
- уравнение искомой прямой.
Второй способ. Искомая прямая проходит через точки 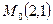 и
и 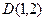 , поэтому её уравнение
, поэтому её уравнение 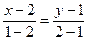 или
или 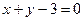 .
.
● Пример 28. Через точку пересечения прямых  и
и 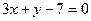 провести прямую,
провести прямую,
3) параллельную оси 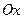 ;
;
3) Первый способ. Если прямая параллельна оси 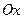 , то общее уравнение этой прямой не содержит переменной
, то общее уравнение этой прямой не содержит переменной 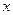 , т.е. в уравнении
, т.е. в уравнении
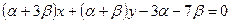 . (3.15)
. (3.15)
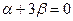 . Откуда при
. Откуда при 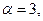
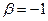 и уравнение искомой прямой
и уравнение искомой прямой 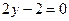 или
или 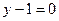 .
.
Второй способ. Так как искомая прямая параллельна оси 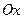 , то её общее уравнение не содержит переменной
, то её общее уравнение не содержит переменной 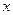 и имеет вид
и имеет вид 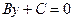 . Точка
. Точка 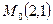 принадлежит этой прямой, поэтому
принадлежит этой прямой, поэтому 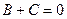 , откуда при
, откуда при 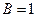 ,
, 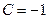 и
и 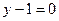 - уравнение искомой прямой.
- уравнение искомой прямой.
● Пример 28. Через точку пересечения прямых  и
и 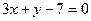 провести прямую,
провести прямую,
4) параллельную оси 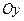 ;
;
4) Первый способ.
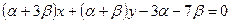 . (3.15)
. (3.15)
Если прямая параллельна оси 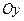 , то
, то 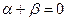 . Полагая
. Полагая 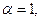 получим
получим 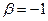 . Уравнение искомой прямой имеет вид
. Уравнение искомой прямой имеет вид 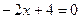 или
или 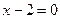 .
.
Второй способ. Так как искомая прямая параллельна оси 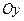 , то вектор
, то вектор 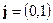 является направляющим вектором этой прямой. Искомая прямая проходит через точку
является направляющим вектором этой прямой. Искомая прямая проходит через точку 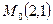 .
.
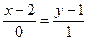 или
или 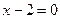 - уравнение искомой прямой.
- уравнение искомой прямой.
● Пример 28. Через точку пересечения прямых  и
и 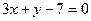 провести прямую,
провести прямую,
5) параллельную прямой 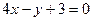 ;
;
5) Первый способ.
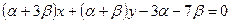 . (3.15)
. (3.15)
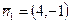 - нормальный вектор данной прямой. Так как прямые параллельны, то
- нормальный вектор данной прямой. Так как прямые параллельны, то 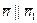 и
и 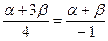 , откуда при
, откуда при 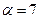
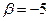 и
и 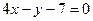 - уравнение искомой прямой.
- уравнение искомой прямой.
Второй способ. Искомая прямая параллельна прямой 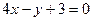 , поэтому вектор
, поэтому вектор 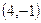 является нормальным вектором обеих прямых. Искомая прямая проходит через точку
является нормальным вектором обеих прямых. Искомая прямая проходит через точку 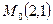 . Учитывая предыдущее, имеем
. Учитывая предыдущее, имеем 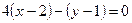 или
или 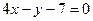 .
.
● Пример 28. Через точку пересечения прямых  и
и 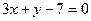 провести прямую,
провести прямую,
6) перпендикулярную прямой 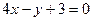 ;
;
6) Первый способ.
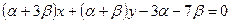 . (3.15)
. (3.15)
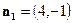 - нормальный вектор данной прямой. Так как прямые перпендикулярны, то
- нормальный вектор данной прямой. Так как прямые перпендикулярны, то 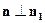 и скалярное произведение нормальных векторов этих прямых равно нулю, т.е.
и скалярное произведение нормальных векторов этих прямых равно нулю, т.е. 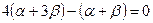 , откуда при
, откуда при 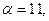
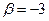 и уравнение искомой прямой
и уравнение искомой прямой 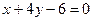 .
.
Второй способ. Нормальный вектор данной прямой 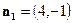 является в этом случае направляющим вектором искомой. Учитывая, что прямая проходит через точку
является в этом случае направляющим вектором искомой. Учитывая, что прямая проходит через точку 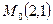 , имеем
, имеем 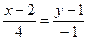 или
или 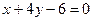 - уравнение искомой прямой.
- уравнение искомой прямой.
● Пример 28. Через точку пересечения прямых  и
и 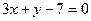 провести прямую,
провести прямую,
7) отсекающую на осях координат равные отрезки.
7) Первый способ.
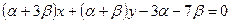 . (3.15)
. (3.15)
Так как прямая отсекает от координатных осей отрезки одинаковой длины, то 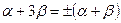 .
.
Если 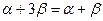 ,то
,то 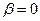 , а
, а 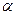 может быть выбрано произвольно. В частности, при
может быть выбрано произвольно. В частности, при 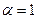 и искомое уравнение прямой
и искомое уравнение прямой 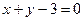 .
.
При 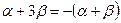 имеем
имеем 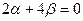 откуда при
откуда при 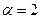 ,
, 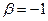 и
и 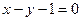 - уравнение искомой прямой.
- уравнение искомой прямой.
Второй способ. Так как прямая отсекает на осях координат равные отрезки, то уравнение прямой в «отрезках» имеет вид 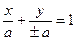 . Координаты точки
. Координаты точки 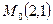 удовлетворяют уравнению
удовлетворяют уравнению 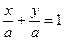 , поэтому
, поэтому 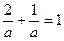 , откуда
, откуда 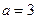 и
и 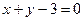 - уравнение одной из искомых плоскостей.
- уравнение одной из искомых плоскостей.
Координаты точки 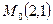 удовлетворяют уравнению
удовлетворяют уравнению 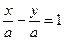 , поэтому
, поэтому 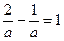 , откуда
, откуда 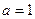 и
и 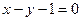 - уравнение плоскости, отсекающая на осях координат равные «отрезки».
- уравнение плоскости, отсекающая на осях координат равные «отрезки».
Ответ: 1) 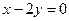 ; 2)
; 2) 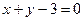 ;3)
;3) 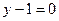 ;
;
4) 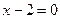 ; 5)
; 5) 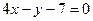 ; 6)
; 6) 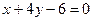 :
:
7) 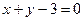 ,
, 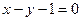 .
.
● Пример 29. Провести прямые, параллельные прямой 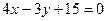 , и отстоящие от неё на расстоянии двух единиц.
, и отстоящие от неё на расстоянии двух единиц.
Решение. Приведём уравнение прямой к нормированному виду. Нормальный вектор данной прямой 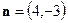 , и свободный член положителен, поэтому нормирующий множитель равен -
, и свободный член положителен, поэтому нормирующий множитель равен - 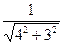 .Тогда
.Тогда 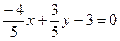 - нормированное уравнение прямой. Так как отклонение
- нормированное уравнение прямой. Так как отклонение 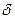 искомых прямых от данной равно
искомых прямых от данной равно 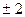 , то
, то 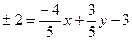 , откуда
, откуда 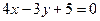 и
и 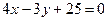 - искомые уравнения.
- искомые уравнения.
Ответ: 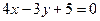 ,
, 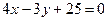 .
.
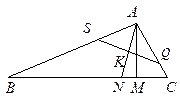 ● Пример 30. Сторона
● Пример 30. Сторона 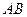 треугольника
треугольника 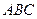 (рис.3.28) лежит на прямой
(рис.3.28) лежит на прямой 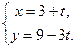 Через вершину
Через вершину 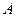 проведены биссектриса и высота. Составить уравнения остальных сторон этого треугольника, если
проведены биссектриса и высота. Составить уравнения остальных сторон этого треугольника, если 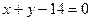 - уравнение
- уравнение
Рис. 3.28 биссектрисы, а точка 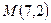 - основание высоты.
- основание высоты.
Решение. Обозначим через 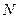 точку пересечения прямой
точку пересечения прямой 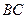 и данной биссектрисы. Точка
и данной биссектрисы. Точка 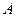 есть общая точка прямых
есть общая точка прямых 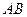 и
и 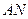 , поэтому её координаты удовлетворяют системе
, поэтому её координаты удовлетворяют системе 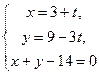 и
и 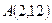 .
.
Вектор 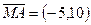 перпендикулярен прямой
перпендикулярен прямой 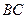 , поэтому в качестве нормального вектора этой прямой может быть выбран вектор
, поэтому в качестве нормального вектора этой прямой может быть выбран вектор 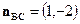 .
.
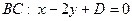 . Точка
. Точка 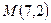 принадлежит этой прямой, поэтому
принадлежит этой прямой, поэтому 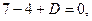
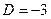 и
и 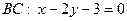 .
.
На прямой 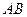 выберем произвольную точку
выберем произвольную точку 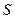 , отличную от
, отличную от 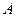 , например,
, например, 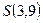 . Пусть точка
. Пусть точка 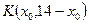 проекция точки
проекция точки 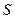 на биссектрису. Тогда вектор
на биссектрису. Тогда вектор 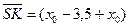 параллелен нормальному вектору биссектрисы
параллелен нормальному вектору биссектрисы 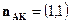 , откуда
, откуда 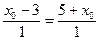 и
и 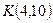 . Найдем точку
. Найдем точку 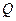 , симметричную точке
, симметричную точке 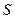 относительно биссектрисы.
относительно биссектрисы.
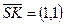 ,
, 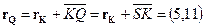 .
.
Сторона 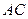 принадлежит пучку
принадлежит пучку 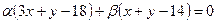
с центром в точке 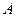 . Точка
. Точка 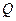 принадлежит прямой
принадлежит прямой 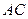 , поэтому
, поэтому 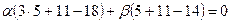 ,
, 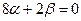 . Полагая
. Полагая 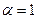 , имеем
, имеем 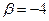 и
и 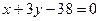 - уравнение стороны
- уравнение стороны 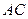 .
.
Ответ: 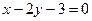 ,
, 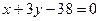 .
.
 2015-06-28
2015-06-28 4546
4546
