Основные понятия. Закон Фурье

Перенос тепла кондукцией в чистом виде имеет место в твердых телах (неподвижных жидкостях и газах), когда температура отдельных его участков неодинакова. Тепло от участков с более высокой температурой передается к участкам с более низкой вследствие энергетического взаимодействия при

соударении микрочастиц (молекул, атомов, электронов) тела при их тепловом движении.

В общем случае температура отдельных частей тела является функцией координат x, y, z и времени t

t = f(x, y, z, t).

Совокупность значений температур всех точек тела в данный момент времени называется температурным полем. При этом, если температура меняется во времени, поле называется нестационарным, если не меняется - стационарным.

Температура может быть функцией одной, двух и трех координат, соответственно этому и температурное поле называется одно-, двух- и трехмерным.

При любом температурном поле в теле всегда имеются точки с одинаковой температурой. Геометрическое место точек с одинаковой температурой называется изотермической

поверхностью. Через каждую точку в теле можно провести только одну изотермическую поверхность. Из определения изотермической поверхности следует, что температура вдоль нее остается постоянной, в любом другом направлении она меняется, причем в направлении нормали к изотермической поверхности наблюдается наибольший перепад температуры на единицу длины.

Предел отношения изменений температуры Dt к расстоянию между изотермами по нормали Dn называется градиентом температуры (рис.2.1.а).

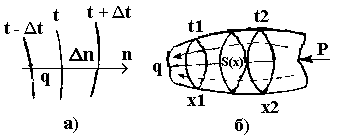
Рис.3.1. Температурный градиент (а) и тепловой поток

в теле (б).

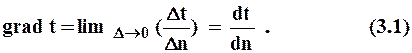За положительное направление градиента температуры принимается направление в сторону возрастания температуры.

Тепло же в теле переносится в сторону убывания температуры. Количество тепла, переносимое в единицу времени через какую-либо поверхность, называется тепловым потоком Р. Тепловой поток, отнесенный к единице площади изотермической поверхности называется плотностью теплового потока q:

где Q - количество тепла, протекающего за время t через

изотермическую поверхность площадью S.

Плотность теплового потока представляет собой вектор, направление которого совпадает с направлением распространения тепла и противоположно направлению вектора градиента температуры (рис. 3.1,6).

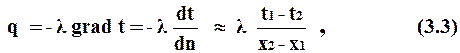Перенос тепла кондукцией описывается законом Фурье, который гласит: плотность теплового потока прямо пропорциональна градиенту температуры, т.е.

где l – коэффициент теплопроводности среды.

Соотношение (3.3) лежит в основе всей современной теории теплопроводности. Из выражений (3.2) и (3.3) следует,

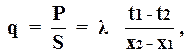откуда непосредственно получаем выражение для коэффициента теплопроводности

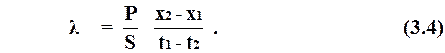Коэффициент теплопроводности представляет количество тепла, протекающее в единицу времени через единицу площади изотермической поверхности при перепаде температур на единице длины нормали, равном одному градусу.

Коэффициенты теплопроводности газов, жидкости и различных материалов лежат в пределах,

Материал	λ [ Вт / м оС]
газы	0,05 - 0,5
жидкости	0,08 - 0,7
Электроизоляционные Материалы	0,02 - 3
Металлы	20 - 400

Коэффициенты теплопроводности зависят от температуры. Так, с повышением температуры коэффициенты теплопроводности газов и изоляционных материалов возрастают, а жидкостей (за исключением воды и глицерина) и большинства металлов –

убывают. У изоляционных материалов коэффициент теплопроводности возрастает и с увеличением влажности, его значение может быть значительно выше, чем сухого материала и воды в отдельности. Из выражения (3.4) получим значение теплового потока

Знаменатель в полученном выражении, равный

называется тепловым коэффициентом.

Значительное число задач теории теплопроводности сводится к определению этого теплового коэффициента.

Найдем выражение коэффициента F в общем виде. Пусть в теле сложной конфигурации протекает неизменный поток Р (рис.3.1.б).

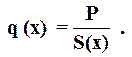Тогда плотность потокачерез любую изотермическую поверхность с координатой x, площадь которой S(x) будет равна

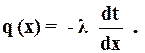С другой стороны, плотность теплового потока через эту же изотермическую поверхность на основании закона Фурье выражается формулой

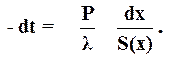Приравнивая правые части и разделяя переменные, получим

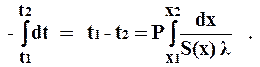Проинтегрировав последнее выражение в пределах от t₁ до t₂, можем записать

Сравнивая полученное выражение с (3.5), имеем

Здесь dx - элемент длины пути теплового потока;

S(х) - аналитическое выражение изотермической

поверхности;

x₁, x₂ - координаты изотермических поверхностей.

Существует аналогия между тепловым потоком и электрическим током. Электрический ток на некотором участке цепи связан с напряжением и сопротивлением этого участка законом Ома

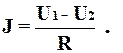Сопоставляя приведенные выражения с (3.5), видим, что аналогом теплового потока является электрический ток, температуры - напряжение, теплового коэффициента – электрическое сопротивление.

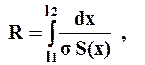Электрическое сопротивление некоторого участка цепи также можно представить в форме, аналогичной (3.7):

где s - удельная электрическая проводимость.

Указанная аналогия справедлива при условии, если между рассматриваемыми изотермическими поверхностями отсутствуют стоки и дополнительные источники энергии. При соблюдении указанного условия тепловой коэффициент называют тепловым сопротивлением и обозначают по аналогии с электрическим сопротивлением через R.

Электрическая аналогия облегчает понимание процесса теплопередачи в сложных конструкциях, позволяет моделировать

тепловые процессы электрическими цепями. Все это упрощает проведение количественного анализа и расчета тепловых цепей, которые проводятся, используя приемы, разработанные для расчета электрических цепей.