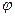Ü| Очевидно, а именно, если уравнение 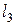 задается (13), то она проходит через точку
задается (13), то она проходит через точку 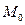 .
.
|Þ Пусть 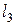 проходит через точку
проходит через точку 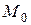 и имеет уравнение
и имеет уравнение 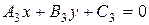 .
.
Возьмем на прямой 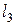 произвольную точку
произвольную точку 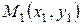 , отличную от точки
, отличную от точки 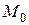 . Положим
. Положим 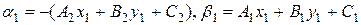 . Покажем, что уравнение для
. Покажем, что уравнение для 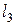 пропорционально (13) с выбранными
пропорционально (13) с выбранными 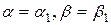 .
.
Т.к. точка 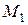 не может одновременно принадлежать прямым
не может одновременно принадлежать прямым 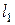 и
и 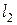 Þ хотя бы одно из
Þ хотя бы одно из 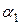 и
и 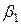 отлично от нуля. Поэтому уравнение
отлично от нуля. Поэтому уравнение 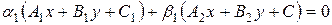 является уравнением первой степени Þ определяет некоторую прямую. По построению эта прямая проходит через точки
является уравнением первой степени Þ определяет некоторую прямую. По построению эта прямая проходит через точки  , а так как через две точки плоскости проходит единственная прямая, то она совпадает с прямой
, а так как через две точки плоскости проходит единственная прямая, то она совпадает с прямой  . Поэтому в силу утверждения 1, уравнения этих прямых пропорциональны, ч.т.д.∎
. Поэтому в силу утверждения 1, уравнения этих прямых пропорциональны, ч.т.д.∎
Замечание. Уравнение (13) называется уравнением пучка прямых, проходящих через точку 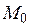 .
.
3°. Прямая линия на плоскости с прямоугольной системой координат. Нормальное уравнение прямой.
Пусть на плоскости задана прямоугольная декартова система координат 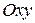 , определяемая ортонормированным репером
, определяемая ортонормированным репером 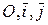 . Пусть прямые
. Пусть прямые 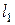 и
и 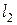 задаются уравнениями (7), (8). Тогда угол между прямыми определяется углом между направляющими векторами и может быть вычислен по формуле
задаются уравнениями (7), (8). Тогда угол между прямыми определяется углом между направляющими векторами и может быть вычислен по формуле
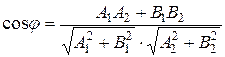 .
.
Отметим, что здесь используется глагол «определяется», так как угол между прямыми принимает значение на промежутке 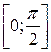 , угол между направляющими векторами –
, угол между направляющими векторами – 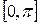 .
.
Получаем, что прямые (7), (8) в прямоугольной системе координат ортогональны Û
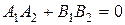 (15)
(15)
Отметим, что только в прямоугольной декартовой системе координат вектор 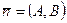 является перпендикулярной к прямой
является перпендикулярной к прямой 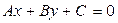
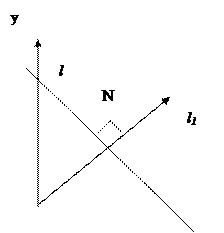
В дальнейшем построим нормальное уравнение прямой на плоскости. Вначале введем уравнение прямой в полярной системе координат. Пусть полярная ось совпадает с Ox и l1 – ось, проходящая через начало координат перпендикулярно прямой l.
|
|

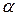
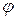
|
Рис.3.
Пусть прямая 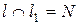 и пусть длина
и пусть длина 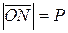 ,
, 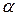 - угол между l1 и
- угол между l1 и 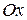 . Если т. М лежит на l1, то очевидно, что проекция
. Если т. М лежит на l1, то очевидно, что проекция 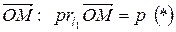
Последнее условие является необходимым и достаточным, для того, чтобы т. М  . Тогда
. Тогда 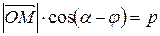 или
или
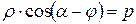 , (16)
, (16)
где 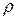 - расстояние от т. М до начала координат,
- расстояние от т. М до начала координат, 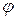 - угол между
- угол между 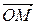 и
и 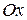 .
.
Другими словами, 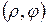 - полярные координаты т. М.
- полярные координаты т. М.
Таким образом, уравнение (16) является уравнением прямой в полярной системе координат. Уравнение (16) можно переписать:
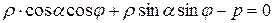 ,
,
где
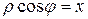 ,
, 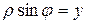 .
.
Здесь 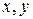 - координаты т. М в соответствующей прямоугольной декартовой системе координат. Получаем:
- координаты т. М в соответствующей прямоугольной декартовой системе координат. Получаем:
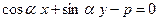 (17)
(17)
– нормальное уравнение прямой на плоскости, где p - длина перпендикуляра, проведенного из начала координат на прямую, 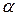 - угол наклона нормали к оси абсцисс.
- угол наклона нормали к оси абсцисс.
Отметим, что 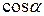 и
и 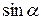 - координаты орта нормали.
- координаты орта нормали.
Покажем, что общее уравнение прямой можно привести к нормальному виду. Пусть прямая l: 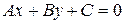 , тогда нормальное уравнение получается умножением на некоторый нормирующий множитель
, тогда нормальное уравнение получается умножением на некоторый нормирующий множитель 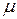 :
: 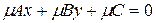 . При этом
. При этом 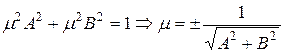 .
.
Знак 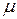 выбирается из условия, что
выбирается из условия, что 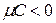 , т.е. если
, т.е. если 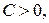 то
то 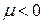 , и наоборот. Если С= 0, то знак
, и наоборот. Если С= 0, то знак 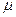 произвольный.
произвольный.
Нормальное уравнение прямой удобно для нахождения расстояния между от произвольной точки плоскости до прямой.

|
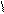
 | |||||
|  | ||||
Рис.4.
Пусть 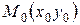 - произвольная точка,
- произвольная точка, 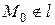 . Пусть
. Пусть 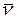 - направляющий вектор прямой l,
- направляющий вектор прямой l, 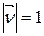 ,
, 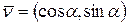 . Очевидно, что расстояние от
. Очевидно, что расстояние от 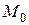 до l определяется по формуле:
до l определяется по формуле: 
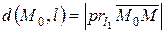 , т.е.
, т.е.
|
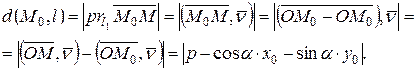
Таким образом, получили, что расстояние от точки до прямой вычисляется следующим образом: в левую часть нормального уравнения этой прямой необходимо подставить координаты точки и полученную величину взять по модулю.
Замечание. Из рисунка видно, что если т. 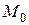 и начало координат лежат по разные стороны от l, то
и начало координат лежат по разные стороны от l, то 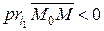 , а если по одну, то
, а если по одну, то 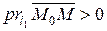 . В первом случае
. В первом случае 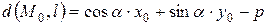 , во втором -
, во втором - 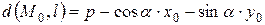 .
.
Последнее может быть использовано для того, чтобы узнать, лежат ли т. 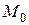 и начало координат по одну сторону или по разные от прямой l.
и начало координат по одну сторону или по разные от прямой l.
Пример. 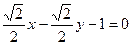 .
.
 2015-06-28
2015-06-28 398
398