Доказательство. |Þ Если прямые 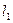и параллельны и не совпадают, то система несовместна, а это эквивалентно (в силу теоремы Кронекера-Конелли) условию

|Þ Если прямые и 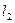параллельны и не совпадают, то система 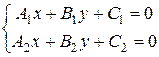несовместна, а это эквивалентно (в силу теоремы Кронекера-Конелли) условию ,

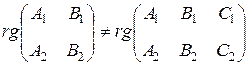Последнее равносильно условию 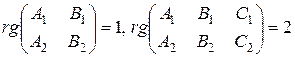, что возможно лишь при выполнении (11).

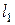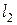Ü| Из первого равенства (11) Þ что прямые и параллельны, а из второго неравенстваÞ система уравнений (7), (8) несовместна Þ прямые параллельны и не совпадают, ч.т.д.∎

Следствие (из утверждений 1 и 2). Прямые 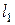и 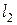пересекаются Û

.

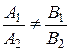(12)

Утверждение 3. Пусть прямые 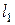и 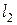, задаваемые уравнениями (7), (8), пересекаются в единственной точке 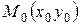. Тогда прямая 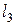проходит через точку 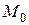Û она задается уравнением

, ,

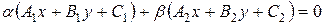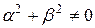(13)

являющимся линейной комбинацией уравнений (7), (8).