Задание 4. Решить задачи.
| Вариант | Условие задачи |
Написать уравнения траектории движения точки 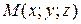 , которая, выйдя из точки , которая, выйдя из точки 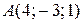 , движется со скоростью , движется со скоростью 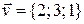 . . | |
Написать уравнения прямой, проходящей через точку 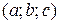 параллельно оси параллельно оси 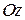 . . | |
Написать уравнения прямой, проходящей через точку 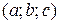 перпендикулярно оси перпендикулярно оси 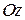 . . | |
Найти угол прямой 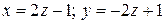 с прямой, проходящей через начало координат и точку с прямой, проходящей через начало координат и точку 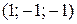 . . | |
Найти угол между прямыми: 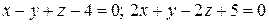 и и 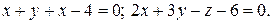 | |
Показать, что прямая 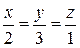 перпендикулярна к прямой перпендикулярна к прямой 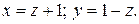 | |
Написать уравнения прямой, проходящей через точку 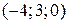 и параллельной прямой и параллельной прямой 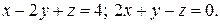 | |
Написать уравнения перпендикуляра, опущенного из точки 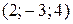 на ось на ось 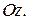 | |
Найти расстояние от точки 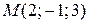 до прямой до прямой 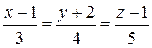 . . | |
Найти расстояние между параллельными прямыми 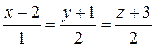 и и 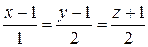 . . | |
Написать уравнения перпендикуляра, опущенного из точки 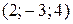 на ось на ось 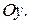 | |
Найти точки пересечения прямой 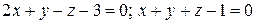 с координатными плоскостями. с координатными плоскостями. | |
Доказать, что прямая 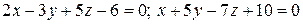 пересекает ось пересекает ось 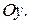 | |
Определить, при каком значении 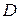 прямая прямая 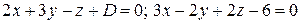 пересекает ось пересекает ось 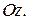 | |
Найти соотношения, которым должны удовлетворять коэффициенты уравнений прямой 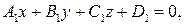 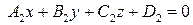 для того, чтобы эта прямая была параллельна оси для того, чтобы эта прямая была параллельна оси 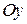 . . | |
Составить уравнения движения точки 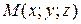 , которая, двигаясь прямолинейно и равномерно, прошла расстояние от точки , которая, двигаясь прямолинейно и равномерно, прошла расстояние от точки 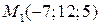 до точки до точки 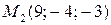 за промежуток времени от за промежуток времени от 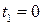 до до 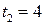 . . | |
Даны вершины треугольника 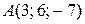 , , 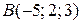 , , 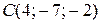 . Составить параметрические уравнения его медианы, проведенной из вершины . Составить параметрические уравнения его медианы, проведенной из вершины 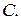 | |
Даны вершины треугольника 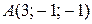 , , 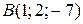 , , 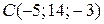 . Составить канонические уравнения биссектрисы его внутреннего угла при вершине . Составить канонические уравнения биссектрисы его внутреннего угла при вершине 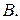 | |
Даны уравнения движения точки 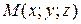 : : 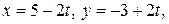 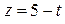 . Определить расстояние, которое пройдет эта точки за промежуток времени от . Определить расстояние, которое пройдет эта точки за промежуток времени от 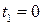 до до 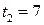 . . | |
Даны прямые 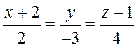 и и 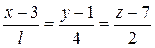 . При каком значении . При каком значении 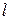 они пересекаются? они пересекаются? | |
Составить уравнения прямой, которая проходит через точку 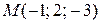 перпендикулярно к вектору перпендикулярно к вектору 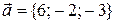 и пересекает прямую и пересекает прямую 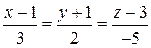 . . | |
Составить уравнения прямой, которая проходит через точку 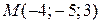 и пересекает две прямые и пересекает две прямые 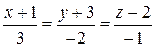 , , 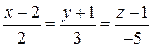 . . | |
Даны уравнения движения точки 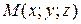 : : 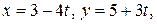 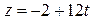 . Определить модуль ее скорости. . Определить модуль ее скорости. | |
Даны вершины треугольника 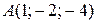 , , 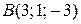 , , 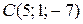 . Составить параметрические уравнения его высоты, опущенной из вершины . Составить параметрические уравнения его высоты, опущенной из вершины 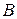 на противоположную сторону. на противоположную сторону. | |
Составить уравнения движения точки 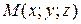 , которая, имея начальное положение , которая, имея начальное положение 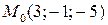 , движется прямолинейно и равномерно в направлении вектора , движется прямолинейно и равномерно в направлении вектора 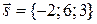 со скоростью со скоростью 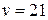 , , | |
Точка 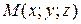 движется прямолинейно и равномерно из начального положения движется прямолинейно и равномерно из начального положения 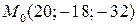 в направлении, противоположном вектору в направлении, противоположном вектору 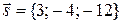 , со скоростью , со скоростью 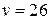 . Составить уравнения движения точки . Составить уравнения движения точки 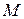 . . | |
Найти соотношения, которым должны удовлетворять коэффициенты уравнений прямой 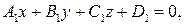 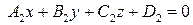 для того, чтобы эта прямая пересекала ось абсцисс. для того, чтобы эта прямая пересекала ось абсцисс. | |
Составить параметрические уравнения общего перпендикуляра двух прямых, заданных уравнениями 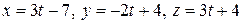 и и 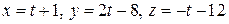 . . | |
Определить, при каком значении 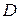 прямая прямая 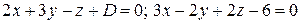 пересекает ось пересекает ось 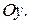 | |
Найти соотношения, которым должны удовлетворять коэффициенты уравнений прямой 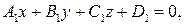 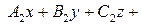 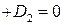 для того, чтобы эта прямая была параллельна оси для того, чтобы эта прямая была параллельна оси 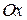 . . |
 2015-06-28
2015-06-28 1030
1030







