Основной системой называется статически определимая и геометрически неизменяемая система, полученная из заданной системы путем отбрасывания всех лишних связей (за исключением абсолютно необходимых). Построение основной системы может быть произведено различными способами. Выбор основной системы является важным этапом расчета, т.к. от него зависит простота и точность расчета рамы.
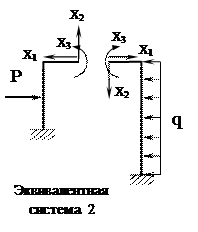
Устранение каких-либо связей не изменяет внутренних усилий, возникающих в системе, и ее деформаций, если к ней прикладываются дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Поэтому, если к основной системе, кроме заданной нагрузки, приложить реакции устраненных связей, то полученная система и заданная система будут эквивалентны. Полученная таким образом система называется эквивалентной системой.
 | |||||||
 | |||||||
 | |||||||
 |
 |
В заданной системе в направлении имеющихся жестких связей (в том числе и тех связей, которые отброшены при переходе к основной системе) перемещений быть не может. Поэтому в эквивалентной системе перемещения по направлениям отброшенных связей должны быть равны нулю. Следовательно, реакции отброшенных связей должны иметь такие значения, при которых перемещения по их направлениям равнялись бы нулю. Таким образом, условие равенства эквивалентной и заданной систем математически сводится к удовлетворению системы n линейных уравнений:
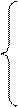 |
δ11Χ1 + δ12Χ2 + …+ δ1nΧn + Δ1Р = 0,
δ21Χ1 + δ22Χ2 + …+ δ2nΧn + Δ2Р = 0,
……………………………………..
δn1Χ1 + δn2Χ2 + …+ δnnΧn + ΔnР = 0.
Эти уравнения являются теми дополнительными уравнениями деформаций (перемещений), которые позволяют раскрыть статическую неопределимость заданной системы. Данные уравнения называются каноническими уравнениями метода сил. Первое из этих уравнений выражает мысль о равенстве нулю перемещения в эквивалентной системе по направлению первой отброшенной связи (по направлению силы или момента Χ1), второе – по направлению второй отброшенной связи и т.д.
Число уравнений равно числу отброшенных связей, т.е. степени статической неопределимости заданной системы.
В системе канонических уравнений в качестве коэффициентов при неизвестных стоят перемещения основной системы, вызываемые единичными силами или моментами, действующими по направлениям отброшенных связей. Коэффициент δij представляет перемещение по направлению связи i, вызванное силой (моментом), равной единице, действующей по направлению связи j. Коэффициенты δij носят название единичных коэффициентов канонических уравнений. Коэффициент Δiр представляет перемещение по направлению связи i, вызванное действием заданной внешней нагрузки. Коэффициенты Δiр называются грузовыми коэффициентами или свободными членами канонических уравнений.
Коэффициенты δii называются главными коэффициентами, а коэффициенты δij – побочными. На основании теоремы о взаимности перемещений δij = δji.
Определяются коэффициенты канонических уравнений с помощью интегралов Мора по формулам:
δij = 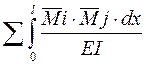
Δiр = 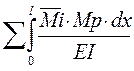
т.к. рамы это конструкции, работающие преимущественно на изгиб, то в выражении интегралов Мора с соблюдением достаточной точности остаются только слагаемые, зависящие от изгибающих моментов.




 Для подсчета коэффициентов вычерчиваются единичные эпюры Мi изгибающих моментов в основной системе, т.е. эпюры от действия Хi = 1. Отдельно строится грузовая эпюра Мр. Единичное перемещение δij вычисляется «перемножением» единичной эпюры Мi на единичную эпюру Мj , а грузовое перемещение – «перемножением» единичной эпюры Мi на грузовую эпюру М р по правилу Верещагина.
Для подсчета коэффициентов вычерчиваются единичные эпюры Мi изгибающих моментов в основной системе, т.е. эпюры от действия Хi = 1. Отдельно строится грузовая эпюра Мр. Единичное перемещение δij вычисляется «перемножением» единичной эпюры Мi на единичную эпюру Мj , а грузовое перемещение – «перемножением» единичной эпюры Мi на грузовую эпюру М р по правилу Верещагина.
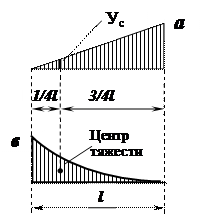
Правило Верещагина: Результат «перемножения» двух эпюр равен произведению площади Ω одной из них на ординату ус другой (обязательно прямолинейной) эпюры, взятую под центром тяжести площади первой эпюры. При перемножении ставится знак плюс, когда эпюра и ордината под центром ее тяжести, взятая из другой эпюры, имеют одинаковые знаки, и минус, - когда разные знаки. (Значения площадей и координаты центров тяжести приведены в приложении 1.)
Результат выполненного по правилу Верещагина перемножения эпюр для определения искомого перемещения следует разделить на величину EI.
 ПРИМЕР
ПРИМЕР


Ω · Ус = ⅓ ·а ·в ·l
Ω = ½ · а ·l
 Ус = ⅔ ·в
Ус = ⅔ ·в
Правилом Верещагина можно пользоваться в том случае, если одна из подынтегральных функций линейна, т.е. одна из «перемножаемых» эпюр прямолинейна, а другая может быть прямолинейной, ломаной или криволинейной.
 ПРИМЕР
ПРИМЕР
Ω · Ус = ⅓ ·в · l ·¼ ·а
Ω = ⅓ ·в · l
 |
Ус = ¼ ·а
Если эпюра моментов на одном участке меняется, т.е. не является непрерывной и образует две различных подынтегральных функции, то такой участок разбивается на два участка и «перемножение» эпюр производится уже по двум соответствующим участкам.
Если обе подынтегральные функции криволинейны на одном участке
длиной l, то для приближенного вычисленияинтеграла Мора можно пользоваться формулой Симпсона.(С помощью формулы Симпсона можно «перемножать» любые эпюры.)
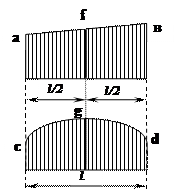 |
l/6 · (a · c + 4 ·f·g + в · d)
f, g – середины эпюр
 2015-06-24
2015-06-24 16638
16638
