Обратная матрица

Если 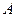– квадратная матрица, то обратной для нее матрицей называется матрица 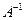, удовлетворяющая условию 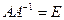, где 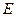– единичная матрица .

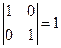Если определитель матрицы равен нулю, то матрица называется вырожденной, а если не равен нулю, то матрица 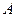называется невырожденной.

Матрица

,

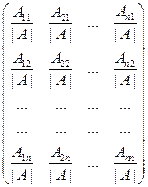где 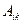– алгебраическое дополнение элемента 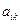невырожденной матрицы, является обратной для .

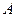Рассмотрим пример составления матрицы, обратной данной:

.

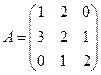1) Вычисляем определитель данной матрицы:

;

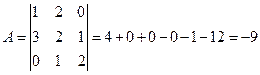2) Вычисляем алгебраические дополнения:

, , ,

, , ,

, , .

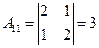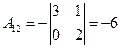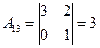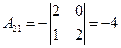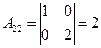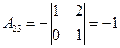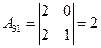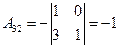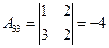3) Составляем матрицу С:

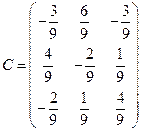
4) Сделав в этой матрице С ее строки столбцами с тем же номером получим:

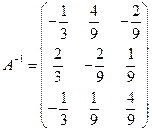– матрица, обратная А.