2015-06-28
330
Систему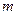 
линейных уравнений с 
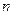неизвестными 
, 
, …, 
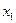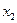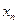можно решить методом исключения неизвестных. Если 
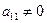, то умножая первое уравнение на 
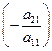и прибавляя ко второму, получаем уравнение, которое не содержит 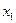. Умножая первое уравнение на 
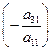и прибавляя к третьему получаем уравнение, также не содержащее 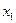. Аналогичным путем преобразуем все остальные уравнения, в результате чего придем к системе, эквивалентной исходной, но не содержащей в 
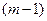уравнении 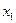. Полагая 
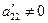и проводя аналогичные преобразования получим систему эквивалентную исходной, но в 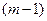уравнение не содержащую 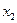. Выполнив ряд аналогичных действий, получим, что в последнем уравнении содержится только 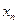. Таким образом, 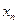– находим из последнего уравнения, 
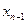– из предпоследнего, и т.д., а 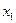– из первого.
Метод последовательного исключения неизвестных применим к любой системе линейных уравнений.
