Нехай задані векторі

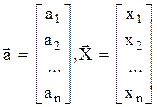
Знайдемо частинну похідну за змінною х_і від скалярного добутку :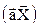

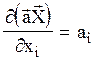
Звідки випливає, що похідна від скалярного добутку векторів 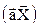за одним із них дорівнює другому вектору:

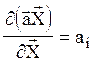
Розглянемо добуток ,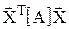

де [A] - квадратна симетрична матриця порядку n,

,

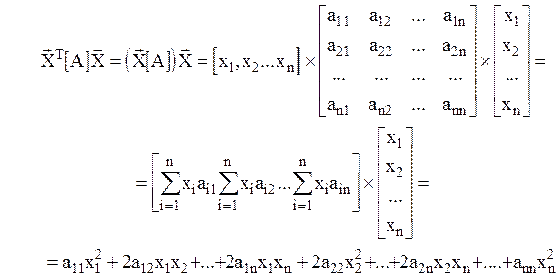Знайдемо частинні похідні за елементами вектора :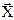

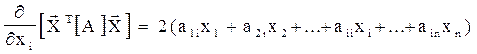
Це подвоєний добуток і-го рядка матриці [A] на вектор - стовпець. Звідки випливає

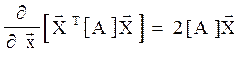
Враховуючи, що [A] 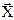= 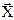^T[A]^T, а також, що для симетричної матриці [A]^T = [A], отримаємо альтернативну формулу

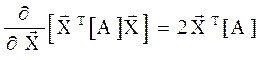
Розглянемо квадратичну матричну форму [ 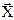^T[A] 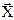] як функцію елементів а_ij матриці [A]. Знайдемо частинну похідну за елементом а_ij.

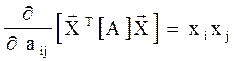
Всього таких частинних похідних n x n. Звідки слідує

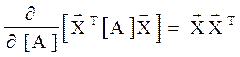
Знайдемо другу частинну похідну за вектором 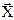від квадратичної форми