Матриці та квадратичні форми

Визначення. Нехай матриця [A] - симетрична. Тоді скалярна функція від (х₁, х₂,..., х_n), де Х = (х₁, х₂,..., х_n)^Т, Х^ТАХ має назву - квадратична форма (х¹0).

Якщо Х^Т[A]X > 0, то квадратна матриця (квадратична форма) [А] - позитивно визначена (³ 0 - невід’ємно визначена).

Якщо Х^Т[A]X < 0, то квадратна матриця (квадратичнa формa) [А] - від’ємно визначена (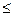 0 - непозитивно визначена).

Скорочений запис цих визначень для матриць [A] ³ 0; [B]< 0.

Визначення. [A]>[B], якщо [A-B]>0, таким чином Х^Т[A-B]X > 0

Аналогічно мождно розглядати інші операції з нерівностями для матриць [ 3 ].

Наприклад, якщо A>B та обидві матриці зворотні, то [A]^-1<[B]^-1.

Властивость матриць, важлива для аналізу в економетрії.

У [A]> 0 ([A] ³ 0) всі власні числа додатні (невід’ємні)

Дійсно, нехай [A]> 0 Х^Т[A]X > 0

Х^ТlX = l Х^ТX > 0, таким чином, власне число l> 0

Якщо матриця [A] - симетрична, то ортогональним перетворенням X=[Q]Z квадратичну форму Х^Т[A]X можливо привести до канонічного вигляду:

Х^Т[A]X = Z^T[Q^T][A][Q]Z = Z^T[l]Z =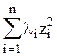

де l_і - власні числа [A] та [Q] - ортогональна матриця складена з власних векторів [A].