Для задания бинарных отношений можно использовать любые способы задания множеств (например, список пар, для которых данное отношение выполняется).
Отношения на конечном множестве обычно задаются списком или матрицей.
Определение: Матрица бинарного отношения, заданного на множестве 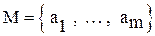 - это квадратная матрица С порядка m, в которой
- это квадратная матрица С порядка m, в которой 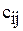 определяется так (i - номер строки, j - номер столбца):
определяется так (i - номер строки, j - номер столбца):
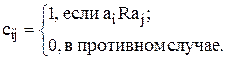
Пример:
Для множества {1, 2, 3, 4, 5, 6} отношения “ 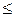 ”, “иметь общий делитель, отличный от 1” и “отношение “
”, “иметь общий делитель, отличный от 1” и “отношение “ 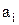 делитель
делитель 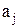 ” имеют матрицы 1, 2 и 3, соответственно.
” имеют матрицы 1, 2 и 3, соответственно.
Матрица 1 Матрица 2 Матрица 3






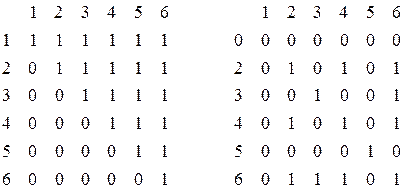
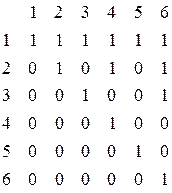
Определение: Для любого множества М отношение Е, заданное матрицей, в которой по главной диагонали стоят “1”, а остальные “0” - называется отношением равенства.
Поскольку отношения на М задаются подмножествами множества 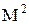 , для них можно определить те же операции, что и над множествами.
, для них можно определить те же операции, что и над множествами.
Например, отношение “находиться на разном расстоянии от начала координат” является дополнением отношения “находиться на одинаковом расстоянии от начала кординат”. Отношение “ 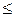 ” является объединением отношений “<” и “=”.
” является объединением отношений “<” и “=”.
Определим еще одну операцию над множествами.
Определение:
Отношение называется обратным к отношению R, если
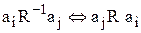 .
.
Из определения следует, что 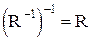 .
.
Для отношения “ 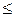 ” обратное к отношению “
” обратное к отношению “ 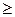 ”.
”.
 2015-06-28
2015-06-28 1106
1106
