Свойства отношений

Определение: Отношение R называется рефлексивным, если для любого 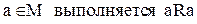. Главная диагональ матрицы такого отношения содержит только единицы.

Определение: Отношение R называется антирефлексивным, если ни для какого 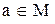не выполняется a R a. Главная диагональ матрицы содержит только нули.

Например, отношения: “ 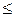”, “иметь общий делитель” - рефлексивны, отношения: “<”, “быть сыном” – антирефлексивны. Отношение “быть симметричным относительно OX” не является ни рефлексивным, ни антирефлексивным. Точка плоскости симметрична сама по себе, если лежит на OX и несимметрична в противном случае.

Определение: отношение R называется симметричным, если для пары 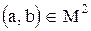из a R b следует b R a (иначе говоря, для любой пары отношение R выполняется в обе стороны или не выполняется вообще).

Матрица симметричного отношения - симметрична относительно главной диагонали: 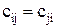для всех .

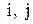Определение: отношение R называется антисимметричным, если из того, что 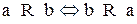следует 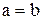(т. е. ни для каких различных элементов множества М отношение R не выполняется).

Матрица антисимметричного отношения не имеет ни одного симметричного относительно главной диагонали единичного элемента.

Например, свойством симметричности обладает отношение “быть симметричным относительно ОХ”; антисимметричным является “ 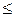”, так как есл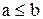и и .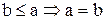

Замечание: R симметрично тогда и только тогда, когда .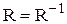

Определение: отношение R называется транзитивным, если для любых a, b, c из множества М из того, что выполняется a R b и b R c следует, что a R c.

Например, отношения: “=“, “жить в одном городе” - транзитивны; отношения: “быть сыном”, “иметь общий делитель” - нетранзитивны. Нетранзитивно и отношение “пересекаться”.

Например, является фактом то, что 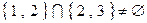и 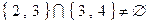, но, тем не менее .

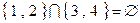Определение: Для любого отношения R отношение 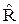, называемое транзитивным замыканием R, определяется следующим образом:

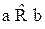, если в М существует цепочка из n элементов 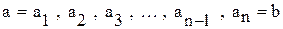, в которой между соседними элементами выполнено отношение R:

.

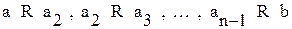Замечание:

Если R - транзитивно, то в определении транзитивного замыкания a R b, поэтому .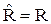

Например, транзитивным замыканием отношения “быть сыном” является отношение “быть прямым потомком”, являющееся объединением отношений “быть сыном”, “быть внуком”, “быть правнуком”, и т. п. Транзитивным замыканием отношения “иметь общую стену” для жильцов дома является отношение “жить на одном этаже”.