Следствие (из Утверждения 3)

Множество P - положительных рациональных чисел (то есть дробей вида 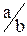, где a и b - натуральные числа) - счетно.

Подчеркнем, что нумерация числового множества Р не имеет ничего общего с упорядочением элементов по величине. В множестве Р нет ни наименьшего элемента, ни двух соседних по величине элементов, однако есть элементы с наименьшим номером и с соседними номерами).

Утверждение 4:

Множество 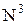и вообще 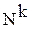для любого натурального k - счетно.

Доказательство: аналогично (3).

Утверждение 5:

Объединение конечного числа счетных множеств 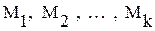- счетно, то есть счетно 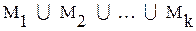, где 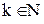- конечное число.

Доказательство:

Перенумеруем сначала все первые элементы множеств, затем все вторые и т. д.

Утверждение 6:

Объединение счетного множества конечных множеств - счетно.

Доказательство:

Нумеруем сначала все элементы первого множества, затем все элементы второго и т. д., т. е. счетно 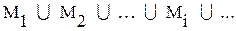, где 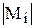- конечное число.

Следствие (из Утверждения 6):

Множество всех слов конечного алфавита - счетно.

А - алфавит, 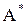- множество всех слов, 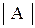- конечное число.

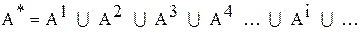
Так как 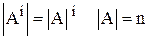, то каждое из этих множеств имеет конечную мощность. Введем обозначение 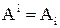, тогда

,

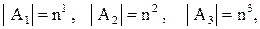то есть выполняется утверждение - счетное объединение конечных множеств - счетно. 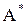- объединение счетного числа множеств, так как между 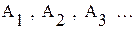и множеством натуральных чисел можно установить взаимно однозначное соответствие.

Утверждение 7:

Объединение счетного множества счетных множеств - счетно, т. е. 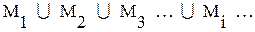- счетное число и 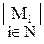- счетное число.

Пример: Объединением счетного множества счетных множеств является, например, 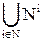- множество всех векторов с натуральными компонентами.

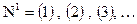
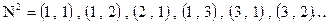
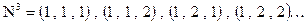
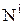- счетное множество, и для любого i 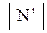- счетно.

Теорема Кантора:

Множество всех действительных чисел отрезка [0, 1] не является счетным.

Доказательство:

При доказательстве используется так называемый диагональный метод Кантора. Докажем от противного.

Пусть это множество точек отрезка 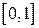счетно, и существует его нумерация (взаимно однозначное соответствие с N). Расположим все числа, изображенные бесконечными десятичными дробями в порядке этой нумерации.

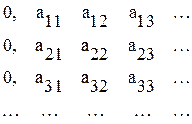
Рассмотрим любую бесконечную десятичную дробь 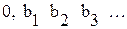такую, что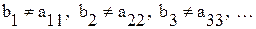

Эта дробь не может войти в указанную последовательность, так как от первого числа она отличается первой цифрой, от второго - второй и т. д. Таким образом, все числа отрезка [0, 1] не могут быть пронумерованы, следовательно, множество всех действительных чисел отрезка [0, 1] несчетно.

Определение: Мощность несчетного множества называется континуум.

Континуальные множества - множества мощности континуум (то есть несчетные множества).

Следствие из теоремы Кантора:

Множество всех подмножеств счетного множества континуально.

Доказательство: 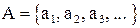- счетное множество. 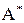- некоторое его подмножество.

Воспользуемся, как в теореме о числе подмножеств конечного множества, представлением подмножества в виде последовательности (но теперь уже бесконечной!) нулей и единиц.

На i - месте последовательности стоит 1, если 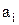входит в данное подмножество.

На i - месте последовательности стоит 0, если 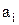не входит в данное подмножество. Получаем 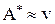(соответствует), где 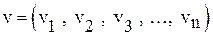следующим образом:

.

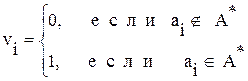Причем, каждый такой вектор единственным образом соответствует десятичной дроби отрезка [0, 1] по принципу: если данную последовательность считать дробной частью двоичного представления числа, то найти его значение в десятичной системе счисления можно по формуле

0,101011...» ...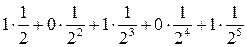

Это взаимно однозначное соответствие между подмножествами счетного множества А и правильными двоичными дробями 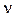, которые, в свою очередь, взаимно однозначно соответствуют континуальному множеству чисел отрезка [0, 1] приводит к выводу о том, что мощность множества V- есть континуум, а, значит, континуальным является и множество подмножеств счетного множества А.