Определения и примеры

Определение. Подмножество 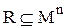называется n - местным отношением на множестве М.

Говорят, что 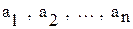находится в отношении R, если 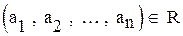. Одноместное отношение – это просто подмножество М. Такие отношения называют признаками: элемент а - обладает признаком R, есл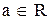и и 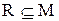. Свойства одноместных отношений это свойства подмножеств М; поэтому для случая n=1 термин “отношение” употребляется редко. Примером трехместного (тернарного) отношения является множество троек нападающих в хоккейной команде. Любой из нападающих находится в этом отношении со всеми теми игроками, с которыми он играет в одной тройке (один нападающий может, вообще говоря, участвовать более, чем в одной тройке).

При n=2 – отношения называются двуместными или “бинарными”. Если a, b находятся в отношении R, это записывается aRb.

Пример

а) отношения, заданные на N:

1) отношение “ 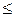” выполняется для пар (7, 9) и (7, 7), но не выполняется для пары (9, 7);

2) отношение “иметь общий делитель 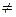1” выполняется для пар (6, 9), (4, 2), (4, 4), (2, 4), но не выполняется для пар (7, 9) и (9, 7);

3) отношение “быть делителем” (т. е. aRb означает: а - делитель b) выполняется для пар (2, 4), (4, 4), (3, 6), (2, 6), но не выполняется для пар (4, 2), (6, 3), (6, 2);

б) отношения, заданные на множестве точек действительной плоскости (на ):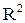

1) отношение: “находится на одинаковом расстоянии от начала координат”, выполняется для пар (3, 4) и 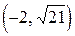(так как расстояние от начала координат до точки а = (3, 4); – 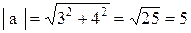; а расстояние от начала координат до точки 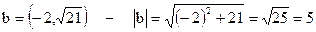), но не выполняется для пар (3, 4) и (1, 6). Это отношение совпадает с отношением “находится на одной и той же окружности с центром в начале координат”;

2) отношение: “находится на разном расстоянии от начала координат” выполняется для тех и только тех точек (пар точек), для которых не выполняется предыдущее соотношение;

3) отношение: “быть симметричным относительно оси OX “ выполняется для всех пар точек 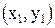и ;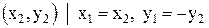

в) отношения, заданное на множестве людей:

“жить в одном городе”, “быть моложе”, “быть сыном”, “быть знакомым”.

Определение: Пусть дано отношение R на М. Для любого подмножества 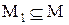естественно определяется отношение 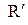, называемое сужением R на 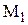, которое получается из R удалением всех пар, содержащих элементы, не принадлежащие 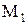. Иначе говоря, 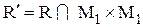. Строго говоря, R и 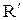- это разные отношения с разными областями определения.