Будем рассматривать двухэлементное множество 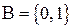 , элементы которого не являются числами в полном смысле этого слова, а интерпретируются как «ложь» и «истина». Считая их логическими переменными, определим следующие функции алгебры двузначной логики.
, элементы которого не являются числами в полном смысле этого слова, а интерпретируются как «ложь» и «истина». Считая их логическими переменными, определим следующие функции алгебры двузначной логики.
Определение:
Отрицанием x назовем функцию 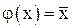 , которая значению аргумента x = 0 ставит в соответствие
, которая значению аргумента x = 0 ставит в соответствие 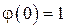 ; а значению аргумента x = 1 ставит в соответствие
; а значению аргумента x = 1 ставит в соответствие 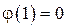 .
.
Определение:
Конъюнкцией элементов 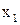 и
и 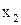 назовем функцию
назовем функцию 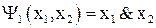 , которая имеет значение 1, только если
, которая имеет значение 1, только если 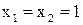 . В остальных случаях конъюнкция равна 0.
. В остальных случаях конъюнкция равна 0.
Определение:
Дизъюнкцией элементов 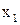 и
и 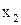 назовем функцию
назовем функцию 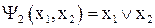 , которая принимает значение 1, если хотя бы один из ее аргументов
, которая принимает значение 1, если хотя бы один из ее аргументов 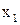 или
или 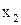 (то есть только
(то есть только 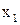 , или только
, или только 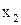 , или
, или 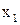 и
и 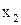 одновременно) равны 1. Дизъюнкция равна нулю тогда и только тогда, когда
одновременно) равны 1. Дизъюнкция равна нулю тогда и только тогда, когда 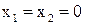 .
.
Определенные так логические функции носят название логических связок «не», «и», «или».
Связь между ними описывается с помощью набора эквивалентностей:
1) 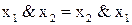 ; 2)
; 2) 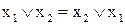 ;
;
3) 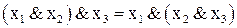 ; 4)
; 4) 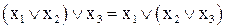 ;
;
5) 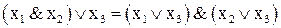 ; 6)
; 6) 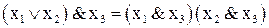 ;
;
7) 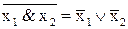 ; 8)
; 8) 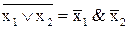 ;
;
9) 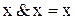 ; 10)
; 10) 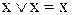 ;
;
11) 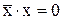 ; 12)
; 12) 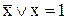 ;
;
13) 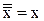 ; 14)
; 14) 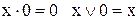 ;
;
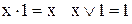 .
.
Любые операции, подчиняющиеся свойствам 1-14, называются булевыми операциями. F алгебры с данным набором операций называются булевыми алгебрами. Так, например, свойства 1-14 будут выполняться и для операций объединения, пересечения и дополнения множеств, если сопоставить
объединение – дизъюнкции;
пересечение – конъюнкции;
дополнение – отрицанию, а вместо 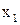 и
и 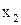 подставить некоторые множества А и В из U (универсального множества).
подставить некоторые множества А и В из U (универсального множества).
Заметим важный факт, что если применить данные операции к логическим функциям 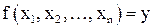 , где
, где 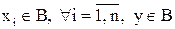 , то результатами тоже будут логические функции. Поэтому связки &,
, то результатами тоже будут логические функции. Поэтому связки &, 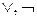 также можно считать и операциями над множеством всех логических функций двузначной логики, обозначаем
также можно считать и операциями над множеством всех логических функций двузначной логики, обозначаем 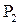 .
.
Тогда алгебра 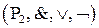 тоже будет булевой алгеброй (булевой алгеброй логических функций), так как для ее операций тоже выполняются соотношения 1-14, где вместо переменных
тоже будет булевой алгеброй (булевой алгеброй логических функций), так как для ее операций тоже выполняются соотношения 1-14, где вместо переменных 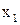 и
и 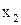 подставлены логические функции
подставлены логические функции 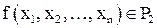 .
.
Если U – некоторое множество элементов мощности n: 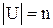 .
.
Определение:  B
B 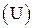 - булеан U – это множество (совокупность) всех подмножеств множества U.
- булеан U – это множество (совокупность) всех подмножеств множества U.
Определение: Алгебра (B 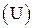 ,
, 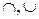
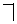 ), несущим множеством которой является множество B
), несущим множеством которой является множество B 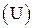 , а операциями – пересечение, объединение и дополнение множеств, называется булевой алгеброй множества U или алгеброй Кантора. Ее тип (2,2,1).
, а операциями – пересечение, объединение и дополнение множеств, называется булевой алгеброй множества U или алгеброй Кантора. Ее тип (2,2,1).
Общий термин ”булева алгебра” для алгебр множеств и логических функций не случаен.
Определение: Всякая алгебра типа (2,2,1) называется булевой алгеброй, если ее операции удовлетворяют основным свойствам булевых операций 1-14.
В алгебре множеств элементами являются подмножества фиксированного (”универсального”) множества U, операции & соответствует пересечение 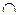 , операции
, операции 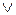 – объединение
– объединение 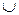 , операции
, операции 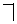 (отрицание) соответствует дополнение; единицей является само множество U, нулем -
(отрицание) соответствует дополнение; единицей является само множество U, нулем - 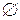 . Справедливость соотношений 1-14 для алгебры множеств можно доказать непосредственно их проверкой. Для этого нужно рассмотреть переменные в них как множества, знаки & и
. Справедливость соотношений 1-14 для алгебры множеств можно доказать непосредственно их проверкой. Для этого нужно рассмотреть переменные в них как множества, знаки & и 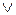 заменить на
заменить на 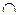 и
и 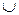 , и показать, что, если какой-либо элемент принадлежит множеству из левой части равенства, то он принадлежит и правой части, и наоборот.
, и показать, что, если какой-либо элемент принадлежит множеству из левой части равенства, то он принадлежит и правой части, и наоборот.
В пункте 4.2. (в теореме о числе подмножеств конечного множества) отмечалось и использовалось взаимно однозначное соответствие 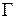 между множеством
между множеством 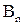 двоичных векторов длины n и множеством B
двоичных векторов длины n и множеством B 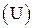 , где
, где 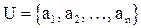 : каждому подмножеству
: каждому подмножеству 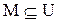 соответствует двоичный вектор
соответствует двоичный вектор 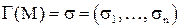 , где
, где 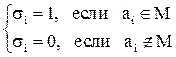 .
.
Булева алгебра 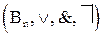 на множестве
на множестве 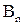 (двоичных векторов) определяется следующим образом: для любых
(двоичных векторов) определяется следующим образом: для любых 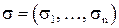 и
и 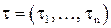
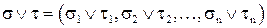
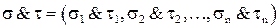
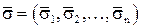 .
.
Поскольку компоненты (разряды) 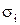 и
и 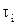 векторов
векторов 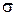 и
и 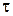 принимают значения 0 и 1, то указанные операции над компонентами – это просто логические операции над двоичными переменными.
принимают значения 0 и 1, то указанные операции над компонентами – это просто логические операции над двоичными переменными.
Определение: Операции над векторами назовем покомпонентными (поразрядными) логическими операциями над двоичными векторами.
Такие операции (наряду с логическими операциями над переменными) входят, в частности, в систему команд любой современной ЭВМ. Выполнение их очень просто: вектор 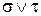 содержит единицы во всех разрядах, в которых есть 1 либо в
содержит единицы во всех разрядах, в которых есть 1 либо в 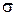 , либо в
, либо в 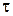 ;
;
- вектор 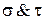 содержит единицы только в тех разрядах, в которых есть единицы и в
содержит единицы только в тех разрядах, в которых есть единицы и в 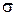 , и в
, и в 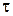 ;
;
- вектор 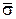 содержит единицы в тех разрядах, в которых
содержит единицы в тех разрядах, в которых 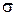 содержит 0 и наоборот.
содержит 0 и наоборот.
Например:
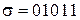
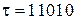 , то
, то 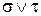 = 11011,
= 11011, 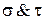 = 01010,
= 01010,
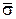 = 10100,
= 10100, 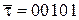 .
.
 2015-06-28
2015-06-28 643
643








