Отношение порядка

Определение: Отношение называется отношением нестрогогопорядка, если оно рефлексивно, антисимметрично, транзитивно.

Определение: Отношение называется отношением строгого порядка, если оно антирефлексивно, антисимметрично, транзитивно. Оба типа отношений называются отношениями порядка.

Определение: Элементы a, b сравнимы по отношению порядка R, если выполняется a R b или b R a.

Определение: Множество М, на котором задано отношение порядка, называется полностью упорядоченным, если любые два элемента М сравнимы.

Определение: Множество М, на котором задано отношение порядка, называется частично упорядоченным, если не любые два элемента М сравнимы.

Пример:

а) отношения “ 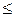” и “ 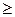” для чисел являются отношениями нестрогого порядка, “<” и “>” - отношениями строгого порядка. Оба отношения полностью упорядочивают множества N и R;

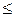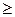б) определим отношения “ ” и “ ” на :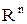

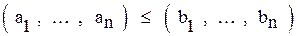, е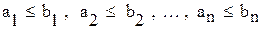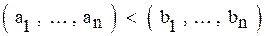сли

;

,если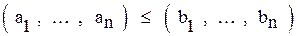

и хотя бы для одной координаты (с номером i) выполнено .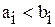

Эти отношения определяют частичный порядок, так как, например:

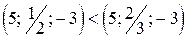и 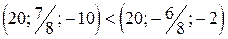, но вектора 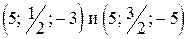– несравнимы;

в) на системе подмножеств множества М отношение “ 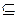” задает нестрогий частичный порядок, а отношение “ 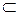” - строгий частичный порядок.

Например, 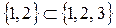, но 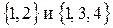- несравнимы;

г) отношение подчиненности на предприятии задает строгий частичный порядок; порядок частичный так как несравнимы сотрудники разных отделов;

д) Лексико - графический порядок.

Пусть в списке букв конечного алфавита А порядок букв зафиксирован, т. е. всегда один и тот же, как, например, в русском и латинском алфавите. Тогда этот список определяет полное упорядочение букв, которое назовем отношением предшествования и обозначим: “ 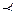”. (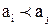, если 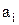предшествует 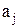в списке букв).

На основе отношения предшествования букв, строится отношение предшествования слов, определяемое следующим образом:

Пусть даны слова 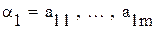и .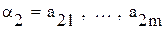

Тогда, 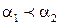тогда и только тогда, когда

1) 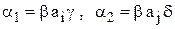, где 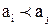( 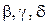- слова возможно непустые, 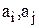- буквы);

2) 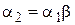, где 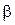- непустое слово.

Это отношение задает полное упорядочение множества всех конечных слов в алфавите А, которое является лексикографическим упорядочением слов.

Пример:

а) упорядочение слов в словарях.

Например, лес 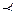лето:

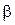= “лес”; “c” 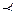“т” и, 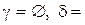”0”, поэтому “лес” в словарях - раньше “лето”;

лес 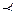лесть:

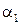= “лес” и 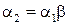, где 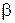= “ть”.

б) если рассматривать числа в позиционных системах счисления (двоичной, десятичной) как слова в алфавите цифр, то их лексико - графическое упорядочение совпадает с обычным, если все сравнимые числа имеют одинаковое число разрядов.