6.1. Алгебры
Определение:
n-арная операция на множестве М – это функция типа
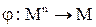 ,
,
где n-арность операции. Операция замкнута относительно множества М по определению, т. е. операция над элементами множества М, и результат тоже элемент М.
Определение: Алгеброй называется множество, вместе с заданной на нем совокупностью операций 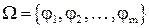 , т. е. система
, т. е. система
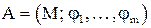 .
.
Определение: М – основное (несущее) множество (носитель алгебры) алгебры А.
Определение: Тип алгебры – вектор арностей операций.
Определение: Сигнатура – совокупность операций W.
Определение: Множество 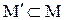 называется замкнутым относительно n-арной операции j на М, если
называется замкнутым относительно n-арной операции j на М, если
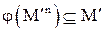 ,
,
т. е. если значения j на аргументе из 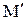 принадлежат
принадлежат 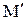 .
.
Определение: Если 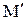 замкнуто относительно всех операций
замкнуто относительно всех операций 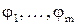 , алгебры М, то система
, алгебры М, то система
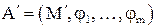
называется подалгеброй алгебры А (при этом 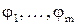 рассматриваются как операции на
рассматриваются как операции на 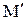 ).
).
Примеры:
1. Определение: Алгебра 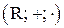 - называется полем действительных чисел.
- называется полем действительных чисел.
Обе операции бинарные, поэтому тип этой алгебры (2,2). Сигнатура 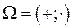 .
.
Подалгеброй этой алгебры является, например, поле рациональных чисел.
2. Пусть 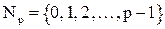 . Определим на
. Определим на 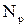 операции:
операции: 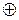 - «сложение по модулю р»,
- «сложение по модулю р», 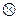 - «умножение по модулю р», следующим образом:
- «умножение по модулю р», следующим образом:
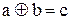 и
и 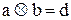 , где с и d – остатки от деления на р чисел а + b и а × b соответственно.
, где с и d – остатки от деления на р чисел а + b и а × b соответственно.
Пусть, например, р = 7, тогда 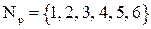 и
и
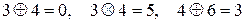 .
.
Часто обозначают: a + b = с (mod p)
a × b = d (mod p).
Определение: Конечным полем характеристики р называется алгебра 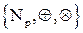 , если р – простое число.
, если р – простое число.
3. Пусть задано множество U.
Определение: Булеаном U называется множество всех подмножеств множества U (обозначается 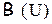 ).
).
Определение: Булева алгебра множеств над U – алгебра 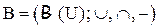 . Ее тип (2,2,1), сигнатура
. Ее тип (2,2,1), сигнатура 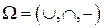 .
.
Элементами основного множества булевой алгебры являются множества (подмножества U).
Для любого 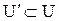
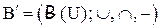 - является подалгеброй В.
- является подалгеброй В.
Например, если 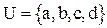 , то основное множество алгебры В содержит 16 элементов; алгебра
, то основное множество алгебры В содержит 16 элементов; алгебра 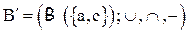 - подалгебра В. Ее несущее множество содержит четыре элемента.
- подалгебра В. Ее несущее множество содержит четыре элемента.
4. Множество F одноместных функций на R, т. е. функции 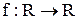 вместе с операцией дифференцирования является алгеброй. Элементы несущего множества – функции типа
вместе с операцией дифференцирования является алгеброй. Элементы несущего множества – функции типа 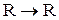 , единственная операция этой алгебры дифференцирования – унарная операция типа
, единственная операция этой алгебры дифференцирования – унарная операция типа 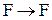 (так как производной функцией на R снова является функция на R).
(так как производной функцией на R снова является функция на R).
Множество элементарных функций замкнуто относительно дифференцирования, поскольку произведение элементарных функций элементарно, следовательно, образуют подалгебру данной алгебры.
5. Рассмотрим квадрат с вершинами в точках 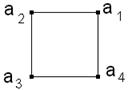
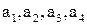 , пронумерованных против часовой стрелки, и повороты квадрата в том же направлении, переводящие вершины в вершины. Таких поворотов бесконечно много: на углы 0,
, пронумерованных против часовой стрелки, и повороты квадрата в том же направлении, переводящие вершины в вершины. Таких поворотов бесконечно много: на углы 0, 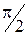 , p,
, p, 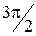 , 2p,
, 2p, 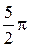 ,..., однако они задают всего 4 различных отображения множества вершин в себя, соответствующие первым четырем поворотам.
,..., однако они задают всего 4 различных отображения множества вершин в себя, соответствующие первым четырем поворотам.
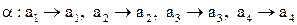 - поворот на углы 0, 2p, 4p,...
- поворот на углы 0, 2p, 4p,...
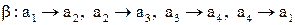 - поворот на углы
- поворот на углы 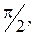
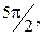
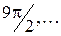
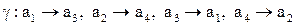 - поворот на углы 0, 3p, 5p,...
- поворот на углы 0, 3p, 5p,...
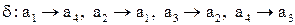 - поворот на углы
- поворот на углы 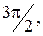
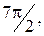
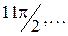
Таким образом, получаем алгебру с основным множеством 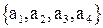 и четырьмя унарными операциями
и четырьмя унарными операциями 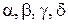 (т. е. сигнатура алгебры
(т. е. сигнатура алгебры 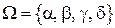 , тип алгебры {1,1,1,1}. Их можно задать таблицей, в которой на пересечении строки номер
, тип алгебры {1,1,1,1}. Их можно задать таблицей, в которой на пересечении строки номер 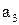 и столбца
и столбца 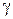 написано значение функции
написано значение функции 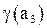 .
.


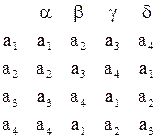
Определение: Тождественной операцией называется операция a, отображающая любой элемент в себя. Тождественная операция соответствует нулевому повороту. Подалгебр в алгебре с одной операцией a, нет.
6. Множество 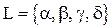 - отображение вершин в себя из предыдущего примера (5), вместе с бинарной операцией композиции “
- отображение вершин в себя из предыдущего примера (5), вместе с бинарной операцией композиции “ 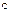 ” отображений образует алгебру (L,
” отображений образует алгебру (L, 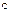 ). Композиция отображений – это последовательное выполнение двух поворотов. Она задается таблицей. В таблице на пересечении строки a и столбца g написан результат
). Композиция отображений – это последовательное выполнение двух поворотов. Она задается таблицей. В таблице на пересечении строки a и столбца g написан результат 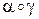 .
.
Таблица Кэли


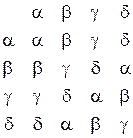
Определение: Такая таблица, задающая бинарную операцию, называется таблицей Кэли. Множество 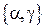 , т. е. повороты на углы 0, p образуют подалгебру алгебры
, т. е. повороты на углы 0, p образуют подалгебру алгебры 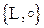 .
.
 2015-06-28
2015-06-28 2162
2162
