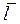Определение. Числовой осью называется ось с выбранным на ней началом отсчета и масштабом.
|
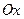 . Точка
. Точка 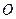 − начало отсчета. Орт числовой оси
− начало отсчета. Орт числовой оси 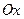 обозначим через
обозначим через 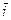 .
.
|
|
|

Пусть  − произвольная точка на числовой оси
− произвольная точка на числовой оси 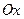 .
.
Определение. Радиусом-вектором точки  на числовой оси называется вектор, началом которого является точка
на числовой оси называется вектор, началом которого является точка 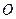 , а концом - точка
, а концом - точка  .
.
Из определения очевидно, что радиус-вектор точки  - закрепленный вектор.
- закрепленный вектор.
Определение. Координатой точки  на числовой оси
на числовой оси 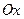 называется проекция радиуса-вектора точки
называется проекция радиуса-вектора точки  на рассматриваемую ось.
на рассматриваемую ось.
Координату точки  на числовой оси
на числовой оси 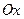 обозначим буквой
обозначим буквой 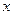 . При этом обычно употребляется следующая запись:
. При этом обычно употребляется следующая запись: 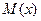 .
.
Итак, по определению,
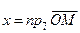 .
.
Можно доказать, что между множеством точек на числовой оси и множеством вещественных чисел существует взаимнооднозначное соответствие, т.е. каждой точке на числовой оси соответствует определенное вещественное число, являющееся координатой этой точки на рассматриваемой оси, и каждому вещественному числу соответствует на числовой оси определенная точка, для которой указанное число является координатой на этой оси.
 2015-06-28
2015-06-28 905
905