Необходимость. Пусть 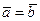 , тогда векторы
, тогда векторы  и
и  можно совместить, и потому, очевидно,
можно совместить, и потому, очевидно, 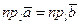 , где
, где  - любая ось.
- любая ось.
Нетрудно показать справедливость утверждения и без совмещения векторов.
Достаточность. Пусть 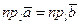 , где
, где  - любая ось. Докажем, что
- любая ось. Докажем, что 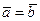 .
.
Предположим противное: 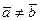 . Убедимся в том, что при этом предположении найдется хотя бы одна такая ось, что проекции векторов
. Убедимся в том, что при этом предположении найдется хотя бы одна такая ось, что проекции векторов  и
и  на эту ось не будут равны между собой.
на эту ось не будут равны между собой.
Рассмотрим два возможных случая:
1). Векторы  и
и  коллинеарны.
коллинеарны.
Совместим начала этих векторов и проведем ось  так, чтобы рассматриваемые векторы оказались расположенными на этой оси.
так, чтобы рассматриваемые векторы оказались расположенными на этой оси.
При этом:
а) Если векторы  и
и  одинаково направлены, то в силу того, что их длины различны (иначе оказалось бы, что
одинаково направлены, то в силу того, что их длины различны (иначе оказалось бы, что 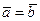 ), концы векторов
), концы векторов  и
и  не совпадут. Очевидно, что тогда составляющие векторов
не совпадут. Очевидно, что тогда составляющие векторов  и
и  по оси
по оси  будут иметь различные длины и, следовательно,
будут иметь различные длины и, следовательно, 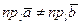 , что противоречит условию утверждения.
, что противоречит условию утверждения.
б). Если векторы  и
и  противоположно направлены, то, очевидно, и составляющие этих векторов по оси
противоположно направлены, то, очевидно, и составляющие этих векторов по оси  имеют противоположные направления. В этом случае проекции векторов
имеют противоположные направления. В этом случае проекции векторов  и
и  на ось являются числами разных знаков, и потому
на ось являются числами разных знаков, и потому 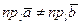 , что противоречит условию утверждения.
, что противоречит условию утверждения.
2). Векторы  и
и  неколлинеарны.
неколлинеарны.
Совместим начала векторов  и
и  и проведем ось
и проведем ось  через общее начало
через общее начало  и
и  перпендикулярно биссектрисе угла
перпендикулярно биссектрисе угла 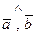 .
.
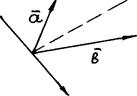
Составляющие векторов  и
и  по оси
по оси  будут иметь противоположные направления. В этом случае проекции векторов
будут иметь противоположные направления. В этом случае проекции векторов  и
и  на ось
на ось  являются числами разных знаков, и потому
являются числами разных знаков, и потому 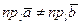 , что противоречит условию утверждения.
, что противоречит условию утверждения.
Итак, предположение, что 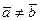 , противоречит условию утверждения, следовательно,
, противоречит условию утверждения, следовательно, 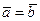 .
.
 2015-06-28
2015-06-28 483
483








