Определение. Говорят, что точка  делит отрезок, соединяющий точки
делит отрезок, соединяющий точки 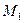 и
и 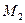 , в данном отношении
, в данном отношении 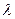 , если вектор
, если вектор 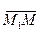 равен произведению вектора
равен произведению вектора 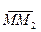 на число
на число 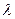 , т.е.
, т.е. 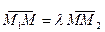 .
.
Согласно определению, точка  делит отрезок, соединяющий точки
делит отрезок, соединяющий точки 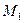 и
и 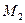 в данном отношении
в данном отношении 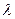 если
если
1) точка  лежит на прямой, проходящей через точки
лежит на прямой, проходящей через точки 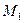 и
и 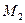 , причем
, причем
а) точка  лежит между точками
лежит между точками 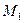 и
и 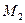 , при
, при 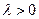 ,
,
б) точка  лежит вне отрезка, соединяющего точки
лежит вне отрезка, соединяющего точки 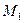 и
и 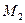 , при
, при 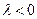
2) 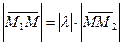
 | |||
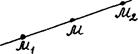 | |||
При этом разумеется, что точка
 не совпадает ни с одной из точек
не совпадает ни с одной из точек 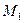 и
и 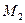
Теорема. Если точка 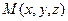 делит отрезок, соединяющий точки
делит отрезок, соединяющий точки 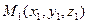 и
и 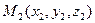 в данном отношении
в данном отношении 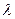 , причем
, причем 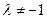 , то для координат точки
, то для координат точки  справедливы следующие равенства:
справедливы следующие равенства:
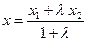 ;
; 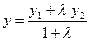 ;
; 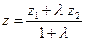
Доказательство. Пусть точка  делит отрезок, соединяющий точки
делит отрезок, соединяющий точки 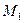 и
и 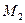 , в данном отношении
, в данном отношении 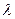 . Тогда по определению
. Тогда по определению 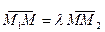 , и потому по отношению к любой оси
, и потому по отношению к любой оси  справедливо равенство
справедливо равенство
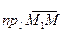
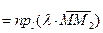 ,
,
или, с учетом теоремы о проекции на ось произведения вектора на скаляр,
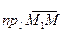
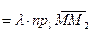 .
.
Возьмем в качестве оси  ось
ось 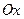 и применим теорему о проекции вектора на числовую ось. При этом получим
и применим теорему о проекции вектора на числовую ось. При этом получим
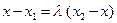 ,
,
откуда следует, что
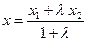 .
.
Вполне аналогично можно доказать справедливость остальных равенств, указанных в формулировке теоремы.
Частный случай. Координаты точки, делящей отрезок пополам (при этом 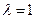 ), равны среднему арифметическому соответствующих одноименных координат концов отрезка, т.е.
), равны среднему арифметическому соответствующих одноименных координат концов отрезка, т.е. 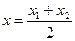 ;
; 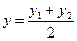 ;
; 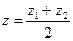 .
.
 2015-06-28
2015-06-28 1761
1761
