Первый критерий коллинеарности двух векторов

Для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы эти векторы были линейно зависимы.

Доказательство. (Необходимость) По условию векторы и коллинеарны. При этом возможны два случая:

1. 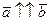. Тогда, по теореме об одинаково направленных векторах, 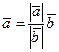, т.е. 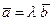, где .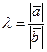

2. 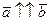. В этом случае, используя теорему о противоположно направленных векторах, имеем 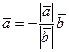, т.е. 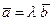. Здесь .

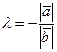Итак, если векторы и коллинеарны, то существует такое числ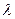о , что 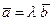, а это равенство, согласно критерию линейной зависимости векторов, означает, что векторы и линейно зависимы. Отсюда, в частности, следует, что любые два вектора, расположенные на одной прямой, линейно зависимы.

(Достаточность.) Пусть векторы и линейно зависимы. Тогда 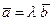, где 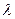- некоторое число. Согласно определению произведения вектора на скаляр, направление вектора 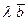в зависимости от знака скаляра 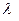либо совпадает с направлением вектора либо противоположно направлению вектора , т.е. вектор , равный 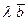, коллинеарен вектору .

Второй критерий коллинеарности двух векторов

Для того, чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы одноименные проекции этих векторов на координатные оси были пропорциональны: .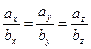

Пропорции 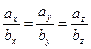формально теряют силу, когда хотя бы один из знаменателей обращается в нуль. Более общей является следующая форма записи факта пропорциональности одноименных проекций рассматриваемых векторов на координатные оси:

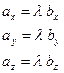
Однако часто используют пропорции .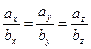

При этом предполагается, что если какой-либо из знаменателей равен нулю, то и соответствующий числитель тоже равен нулю.

Доказательство. (Необходимость) Если векторы и коллинеарны, то согласно первому критерию коллинеарности двух векторов, векторы и линейно зависимы, а потому 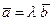. Из этого равенства следует, что 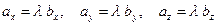, т.е. .

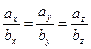(Достаточность) Пусть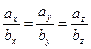

Положим каждое из этих отношений равным 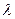. Тогда .

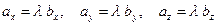Если же наряду с этими равенствами воспользоваться теоремой о разложении вектора по координатным ортам 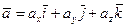, то получим 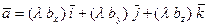, или, согласно свойствам операции умножения вектора на скаляр, 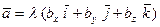, т.е. .

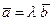Следовательно, векторы и линейно зависимы, и потому, согласно первому критерию коллинеарности двух векторов, векторы и коллинеарны, что и требовалось доказать.