Определение. Направляющими косинусами вектора  называются косинусы углов между координатными осями и рассматриваемым вектором
называются косинусы углов между координатными осями и рассматриваемым вектором  , т.е.
, т.е. 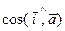 ,
, 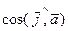 ,
, 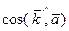 .
.
Теорема. Орт вектора может быть представлен в виде линейной комбинации координатных ортов с соответствующими направляющими косинусами этого вектора, т.е. 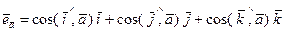
Доказательство. По теореме о разложении вектора по координатным ортам
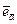
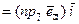
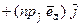
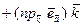 и так как
и так как 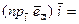
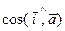 ,
, 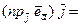
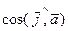 ,
, 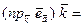
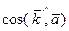 , то
, то 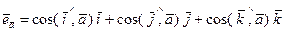
Разложение радиуса-вектора точки по координатным ортам
Теорема. Радиус-вектор точки  может быть представлен в виде линейной комбинации координатных ортов с декартовыми координатами точки
может быть представлен в виде линейной комбинации координатных ортов с декартовыми координатами точки  , т.е.
, т.е.
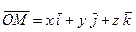 ,
,
где 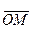 - радиус-вектор точки
- радиус-вектор точки  ,
, 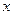 ,
, 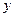 ,
, 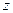 - декартовы координаты точки
- декартовы координаты точки  .
.
Доказательство. Всякий вектор может быть представлен в виде:
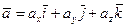 .
.
Применительно к радиусу-вектору точки  имеем
имеем
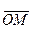
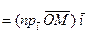
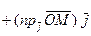
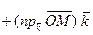
Согласно определению декартовых координат точки 
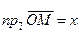 ,
, 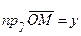 ,
, 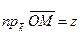 ,
,
и потому 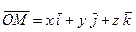 .
.
 2015-06-28
2015-06-28 920
920








