2015-06-28
572
Определение. Векторным произведением упорядоченной пары векторов 
и 
называется новый вектор, обозначаемый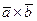 
и определяемый следующими условиями:
1. Модуль векторного произведения векторов и равен произведению модулей этих векторов на модуль синуса угла между векторами и , то есть
.
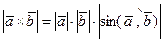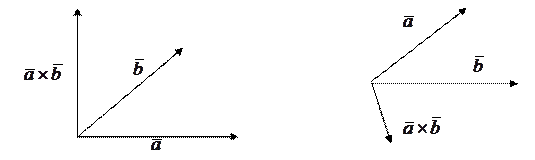
2. Направление векторного произведения векторов и определяется следующим образом:
1) векторное произведение векторов и перпендикулярно каждому из них;
2) упорядоченная тройка векторов , , 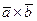является правой.
