 На векторах
На векторах  ,
,  ,
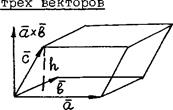
,  построим параллелепипед (см. рис.), объем которого обозначим через
построим параллелепипед (см. рис.), объем которого обозначим через 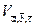 .
.
Теорема. Модуль смешанного произведения векторов  ,
,  ,
,  численно равен объему
численно равен объему 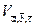 параллелепипеда, построенного на векторах
параллелепипеда, построенного на векторах  ,
,  ,
,  :
:
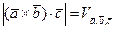 .
.
Доказательство. Согласно свойству 2 скалярного произведения векторов 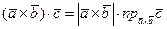 или, с учетом геометрического истолкования модуля векторного произведения двух векторов,
или, с учетом геометрического истолкования модуля векторного произведения двух векторов, 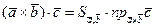 . Тогда
. Тогда 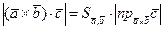 , нo
, нo 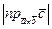 есть высота рассматриваемого параллелепипеда (см, рис.). Обозначая высоту параллелепипеда через
есть высота рассматриваемого параллелепипеда (см, рис.). Обозначая высоту параллелепипеда через 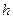 , получим
, получим 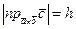 и
и 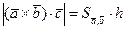 . Так как
. Так как 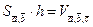 , то приходим к выводу, что действительно
, то приходим к выводу, что действительно 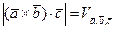 .
.
 2015-06-28
2015-06-28 534
534








