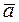Свойства смешанного произведения трех векторов

1. Смешанное произведение упорядоченной тройки некомпланарных векторов положительно, если эта тройка векторов является правой и отрицательно, если рассматриваемая тройка векторов является левой, то есть, если , , - некомпланарная тройка векторов, то

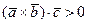, если , , - правая тройка векторов;

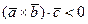, если , , - левая тройка векторов.

Смешанное произведение компланарной тройки векторов равно нулю, то есть, если , , - компланарные векторы, то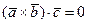

Доказательство. По определению скалярного произведения векторов

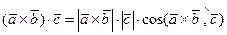
Знак смешанного произведения векторов , , совпадает со знаком .

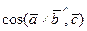Рассмотрим два случая.

1) , , - правая тройка векторов.

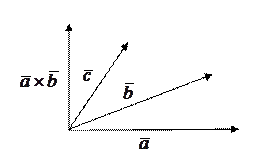
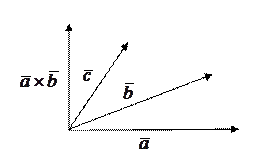
Согласно определению векторного произведения векторов, векторы , , 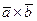также образуют правую тройку векторов, и потому в рассматриваемом случае 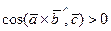, следовательно,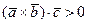

2) , , - левая тройка векторов.

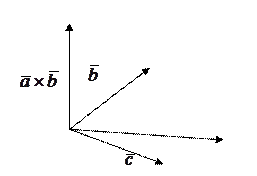
В этом случае 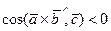и потому .

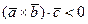Допустим теперь, что , , - компланарные векторы. Тогда 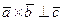и .

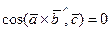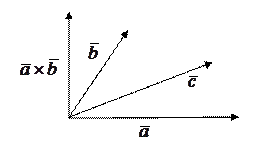
Следовательно, для компланарных векторов , , имеет место равенство .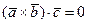

2. Смешанное произведение трех векторов обладает свойством цикличности, то есть

.

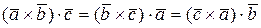Доказательство. Модуль каждого из смешанных произведений 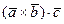, , 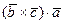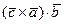численно равен объему параллелепипеда, построенного на векторах , , , значит, модули рассматриваемых смешанных произведений равны между собой. Кроме того, если , , - некомпланарные векторы, то упорядоченные тройки векторов , , ; , , и , , , являются тройками одинаковой ориентации, и потому, на основании предыдущего свойства, соответствующие смешанные произведения имеют один и тот же знак. Из изложенного и следует, что .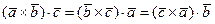

В случае, если , , - компланарные векторы, все рассматриваемые смешанные произведения равны нулю и, следовательно, равны между собой.

Учитывая свойство цикличности, смешанное произведение 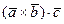с часто записывают в виде .

3. При перестановке двух векторов смешанное произведение трёх векторов меняет знак, то есть

;

;

.

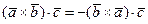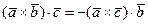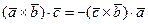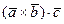Доказательство. Убедимся в справедливости первого равенства. Если , , - некомпланарные векторы, то упорядоченные тройки векторов , , и , , являются тройками противоположной ориентации, и потому, согласно свойству 1 смешанного произведения трёх векторов, и 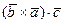имеют разные знаки. Учитывая, кроме того, равенство модулей этих смешанных произведений, получим .

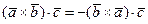Если же , , - компланарные векторы, то рассматриваемые смешанные произведения равны нулю, следовательно, и в этом случае доказываемое утверждение справедливо.

Аналогично можно проверить справедливость остальных равенств.