Если в высокочастотной области (ω> 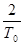 ) передаточная функция непрерывной части апраксимируется выражением (21), то частотная характеристика имеет свои особенности.
) передаточная функция непрерывной части апраксимируется выражением (21), то частотная характеристика имеет свои особенности.
Wвч (p) = 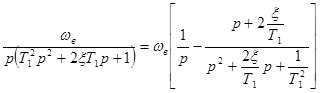 , где
, где 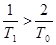 . (21)
. (21)
Рассмотрим частный случай:
1) ξ=0, тогда
Wвч (p) = 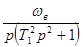 , дискретная передаточная функция
, дискретная передаточная функция
Wвч (z) = 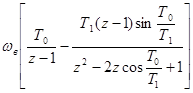 ,
,
а дискретная частотная функция
Wвч (jλ) = 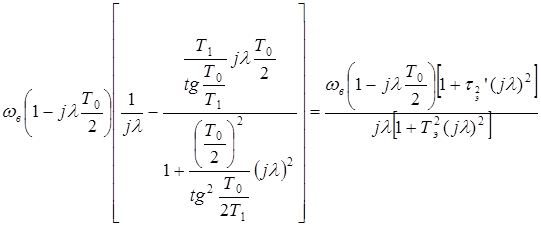 ,(22)
,(22)
где τэ и Тэ — эквивалентные постоянные времени.
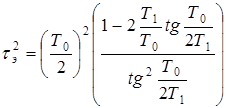 ,
,
|
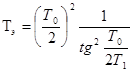 .
.
|
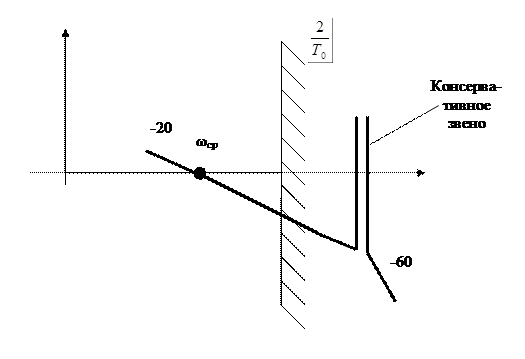
Рисунок 26 – ЛАЧХ при наличии консервативного звена
2) ξ≠0, тогда дискретная частотная функция определяется выражением (23):
W вч(jλ) = 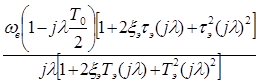 , (23)
, (23)
где 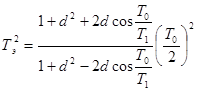
d= 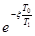 ,
,
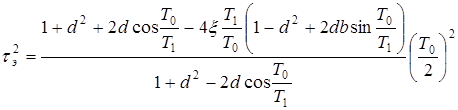 .
.
β= 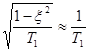 при малых ξ.
при малых ξ.
ξэ = 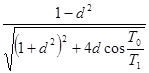 ; b=
; b= 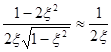 при малых ξ.
при малых ξ.
Можно вывести аналитические соотношения для различных видов ЛАЧХ высокочастотной области.
Так, если
Wвч (р) = 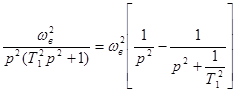 →
→
Wвr (jλ) = 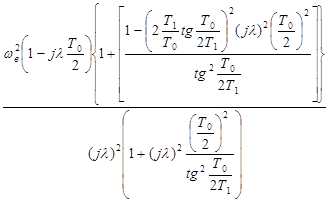 (24)
(24)
При построении ЛАЧХ в области высоких частот необходимо учитывать сумму малых постоянных времени и дополнительный множитель 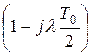 , который приводит к подъему ЛАЧХ на высоких частотах, обеспечивая нулевой наклон.
, который приводит к подъему ЛАЧХ на высоких частотах, обеспечивая нулевой наклон.
Для упрощения процесса синтеза как и для непрерывных систем вводят понятие типовых ЛАЧХ систем с ЦВМ (рис. 27) и типовых W(p) и W(jl) (табл. 1).
а)
| Цифровой системы | Статические | 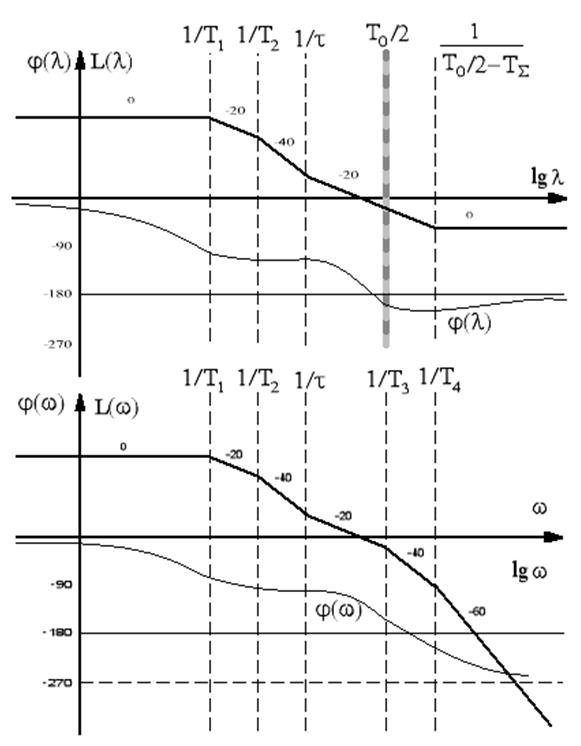
|
| Непрерывной системы |
б)
| Цифровой системы | Астатические | 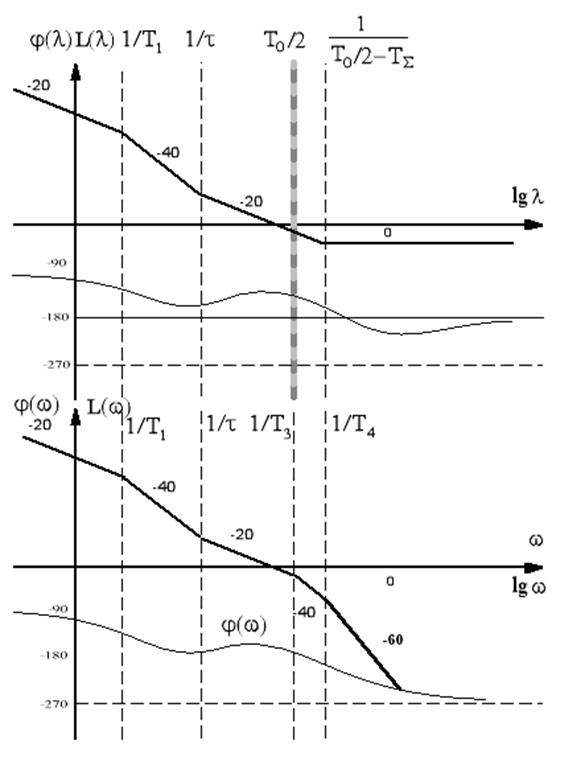
|
| Непрерывной системы |
в)
| Цифровой системы | Астатические | 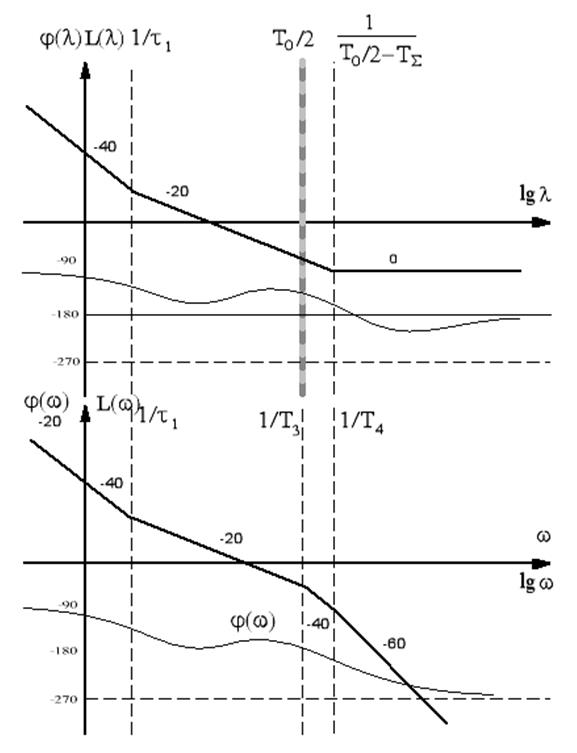
|
| Непрерывной системы |
Рисунок 27 – Типовые ЛАЧХ цифровых и непрерывных систем
Таблица 1 – Типовые передаточные функции
| Тип ЛАЧХ | Передаточные функции | |
| Цифровой следящей системы | Непрерывной части системы | |
| I. | 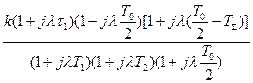
| 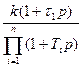
|
| II. | 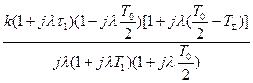
| 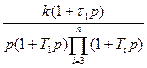
|
| III. | 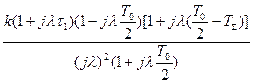
| 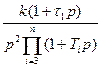
|
 2015-06-28
2015-06-28 557
557

 )
)







