Построение прямой уровня

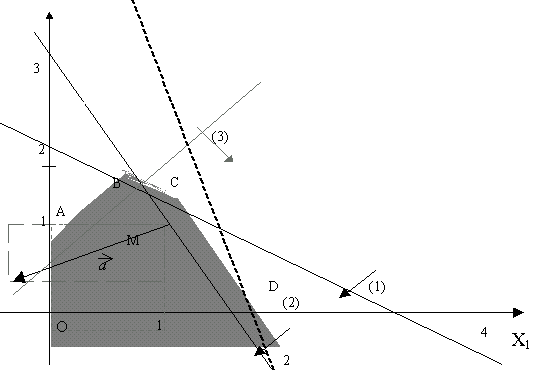
Возьмем произвольную точку, принадлежащую области допустимых решений - ОАВСD, например, точку М с координатами (1; 1). Подставим координаты точки М в функцию F.

Получается F(1; 1)=-3*1 - 1=- 4.

Прямая уровня будет иметь следующий вид: -3x₁ - x₂=- 4

Найдем две точки этой прямой - (1; 1) и (0; 4) (если x₁=0, то x₂=4). Построим прямую уровня. Вектор а{-3; - 1}, отложенный от точки М указывает направления возрастания функции F. Минимизируем данную функцию F.

Минимизация целевой функции F.

Так как построенный вектор - является вектором а, указывающем направление возрастания функции F, то передвижение прямой уровня в направлении, обратном вектору а позволит нам найти точку минимума. В нашем случае - это точка D. Координаты точки D равны (2; 0)

Подставляя кординаты точки минимума в функцию F, получим

F(2; 0)= -3*2 - 0= - 6

Ответ: Минимум функция F равен - 6, и он достигается в точке с координатами (2;0)

Рисунок 2.3.7.

Теперь исследуем вопрос о разрешимости двумерной задачи линейного программирования. Исследуем вначале область допустимых решений. Понятно, что область допустимых решений существует только тогда, когда ограничения не противоречивы. Если ограничения противоречивы, то область допустимых решений не существует, следовательно, данная задача не имеет решений.