Пример 3. Решить графическим способом следующую двумерную задачу линейного программирования

Решить графическим способом следующую двумерную задачу линейного программирования:

Рисунок 2.3.8.

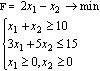
Решение:

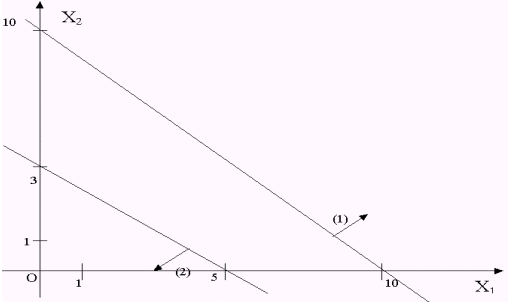
Построение области допустимых решений целевой функции F.

Первое ограничение:

x₁+x₂>=10

x₁+x₂ = 10 (1)

При x₁=0 x₂=10 (0; 10)

При x₂=0 x₁=10 (10; 0)

Второе ограничение:

3x₁+5x₂>=15

3x₁+5x₂ = 15 (2)

При x₁=0 x₂=5 (0; 5)

При x₂=0 x₁=3 (3; 0)

Ограничения задачи противоречивы, поэтому области допустимых решений не существует, следовательно, данная задача неразрешима.

Рисунок 2.3.9.

Рассмотрим случай, когда область допустимых решений существует. Здесь возможны два варианта:

1. Область допустимых решений ограниченна со всех сторон (примеры №1,2);

2. Область допустимых решений неограниченна с какой-либо стороны.

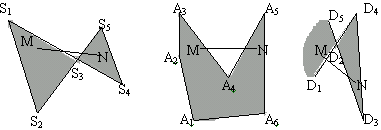
Примечание - Область допустимых решений всегда является выпуклым множеством. Множество S называется выпуклым, если для любых двух точек M и N этого множества весь отрезок MN содержится в множестве S. На рисунках изображены примеры выпуклых (рис. 1) и невыпуклых множеств (рис. 2).

Рисунок 2.3.10.

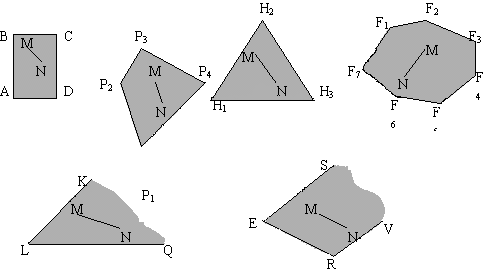
Рисунок 2.3.11.

Если область допустимых решений ограничена (она представляет собой замкнутый выпуклый N - угольник), то задача разрешима и экстремальное значение достигается в какой - либо вершине области допустимых решений. Исключение составляет тот случай, когда прямая уровня параллельна одной из сторон области допустимых решений, и по условию задачи ее надо перемещать именно в направлении этой стороны. Тогда оптимальное решение будет достигаться в любой точке, принадлежащей данной стороне.

Рассмотрим этот случай на примере.