Пусть задан ряд распределения 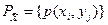 дискретного случайного вектора
дискретного случайного вектора 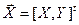 , найдены ряды распределения
, найдены ряды распределения 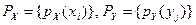 случайных величин
случайных величин 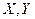 и их числовые характеристики – MX, MY, DX, DY, σX, σY.
и их числовые характеристики – MX, MY, DX, DY, σX, σY.
Определение 1. (Математическое ожидание, дисперсия и С.К.О. случайного вектора).
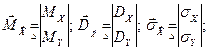 (1)
(1)
Определение 2. Если числовая функция двух переменных g(x,y) определяет на 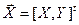 случайную величину
случайную величину
Z =g( 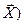 , математическим ожиданием Z называется число M[Z=g(X,Y)]
, математическим ожиданием Z называется число M[Z=g(X,Y)] 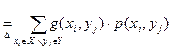 . (2)
. (2)
Теорема. Если случайные величины 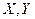 имеют конечные мат. ожидания, мат. ожидание линейной комбинациислучайных величин равно линейной комбинацииих мат. ожиданий
имеют конечные мат. ожидания, мат. ожидание линейной комбинациислучайных величин равно линейной комбинацииих мат. ожиданий
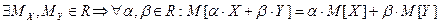 (3)
(3)
Для доказательства запишем определение (2) и упорядочим суммирование в каждом слагаемом
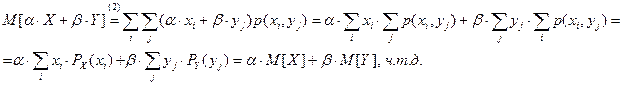
è 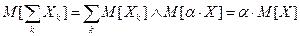 (3’)
(3’)
Определение 3.
Ковариационным моментом случайных величин 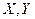 - координат случайного вектора называется число
- координат случайного вектора называется число
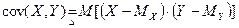 (4)
(4)
Коэффициентом корреляции случайных величин 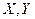 называется безразмерная величина
называется безразмерная величина
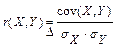
 2015-06-28
2015-06-28 757
757








