Cледствия

1. Если в (4) раскрыть скобки, из определения (2), свойств (3’) и условия 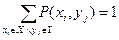получим равносильную формулу для cov(X,Y) 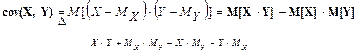(4’)

2.

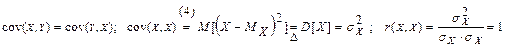
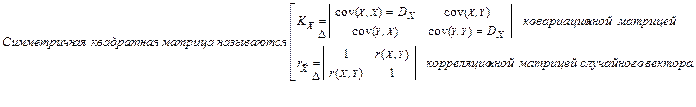
Зависимость и коррелированность случайных величин.

ТВ: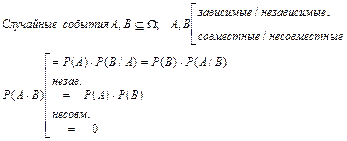

Определение 1 Случайные величины X,Y называются независимыми, если их совместное распределение равно произведению распределений этих случайных величин. Иначе X,Y называются зависимыми.
ДСВ: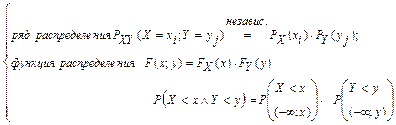
НСВ: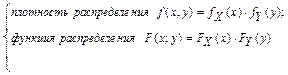

Определение 2 Случайные величины X,Y называются некоррелированными, если их ковариационный момент (и коэффициент корреляции) равен нулю: cov(X,Y)=r(X,Y)=0. Иначе X,Y называются коррелированными.