Олигополия

В настоящее время слово «олигополия» используется экономистами как термин, обозначающий определенный тип строения рынка, при котором сторона предложения представлена небольшим числом сравнительно крупных предприятий-продавцов однородной продукции или близких субститутов.

Крупный размер предприятий олигополистов — прямое следствие их немногочисленности, точно так же, как малость совершенно конкурентных предприятий является следствием их множественности.

Как известно на рынках совершенной конкуренции и монополии отсутствуют все виды соперничества между продавцами. Ясно, что монополист, спрос на продукцию которого представляет в то же время и весь отраслевой спрос, не имеет реальных соперников на своем рынке, по определению. У него могут быть лишь потенциальные соперники, но от угрозы вторжения их на рынок он может укрыться за барьером на вход, естественным, легальным или искусственно выстроенным им самим. Если же такому потенциальному сопернику все же удастся преодолеть барьер на вход и войти на данный рынок (в отрасль), монополист утратит свою абсолютную рыночную власть, строение рынка изменится, монополия перестанет быть монополией. В случае совершенной конкуренции отсутствие соперничества продавцов является, как мы помним, просто следствием их малости и множественности, в силу которых ни одно совершенно конкурентное предприятие не может сколь-либо ощутимо повлиять на уровень рыночной цены.

Особенность олигополии, как специального типа строения рынка, заключается во всеобщей взаимозависимости поведения предприятий-продавцов. Предприятие-олигополист не может не считаться с тем, что соотношение между выбранным им уровнем цены и количеством продукции, которое оно сможет по этой цене продать, зависит от поведения его соперников, которое в свою очередь зависит от принятого им решения. Поэтому олигополист не может рассматривать кривую спроса на свою продукцию как заданную. А это значит, что олигополист, стремящийся к максимизации прибыли, не может воспользоваться известным рецептом уравнивания предельных затрат и предельной выручки. Ведь величина предельной выручки зависит от характера функции спроса, которая для олигополиста неизвестна.

Именно это, «незаданность» функции спроса на продукцию олигополиста в момент принятия им решения об уровне цены и/или выпуска, и предопределяет особенности рынка, имеющего олигопольное строение. Олигополист должен поэтому сделать (или принять) некоторые предположения о реакции своих соперников на принимаемые им решения и предпринимаемые действия, а также и об обратном воздействии реакции соперников на результаты своих решений. Таким образом, общая взаимозависимость предприятий-олигополистов представляет главную черту олигопольных рынков. Ясно, что результаты соперничества на таких рынках в большой мере зависят от характера допущений о реакции соперников на действия друг друга, а они могут быть существенно отличными. Поэтому-то и не существует единой, всеобщей модели олигополии, как это имеет место в случае совершенной конкуренции или монополии. Вместо этого известно несколько моделей олигополии, различающихся характером предположений олигополистов и особенностями их взаимоотношений.

Прежде всего олигопольные рынки различают по тому, действуют ли их участники-олигополисты совершенно независимо друг от друга, на свой страх и риск или же, напротив, они вступают в сговор, который может быть явным, открытым или тайным, скрытым. В первом случае обычно говорят о некооперированной, во втором о кооперированной олигополии.

Очевидно, что при анализе поведения олигополистов, действующих совершенно независимо друг от друга, определяющее значение имеют различия в предположениях относительно реакции соперников. В зависимости от того, выбирает ли олигополист в качестве управляемой переменной величину выпуска или цену, различают олигополию предприятий, устанавливающих величину выпуска, или просто количественную олигополию, и олигополию предприятий, назначающих цену или ценовую олигополию.

Допущения, на которых базируется вычленение олигополии как особого типа строения рынка, немногочисленны и более реалистичны по сравнению с допущениями, лежащими в основе моделей совершенной конкуренции и монополии.

1. Если в модели совершенной конкуренции однородность продукции, выпускаемой (продаваемой) разными экономическими агентами, является одним из важнейших допущений, а неоднородность, или дифференциация, продукции является определяющим допущением в модели монополистической конкуренции, то в случае олигополии продукция может быть как однородной, так и неоднородной. В первом случае говорят о классической, или однородной, олигополии, во втором — о неоднородной, или дифференцированной, олигополии. В теории удобнее рассматривать однородную олигополию, но если в действительности отрасль выпускает дифференцированную продукцию (множество субститутов), мы можем в аналитических целях рассматривать это множество субститутов как однородный продукт.

2. Немногочисленность продавцов, которым противостоит множество мелких покупателей. Это значит, что покупатели на олигопольном рынке являются ценополучателями, каждый из них убежден, что его поведение не влияет на рыночные цены. С другой стороны, сами олигополисты являются «ценоискателями», каждый из них понимает, что его поведение оказывает ощутимое влияние на цены, которые могут получить за свою продукцию соперники.

3. Возможности входа в отрасль (на рынок) варьируют в широких пределах, от полностью блокированного входа (как в модели монополии) до совершенно свободного (как в модели совершенной конкуренции). Возможность регулировать вход, равно как и необходимость учитывать при принятии решений возможную реакцию соперников, формирует стратегическое поведение олигополистов.

Рассмотрим дуополию, субъекты которой — обозначим их индексами 1 и 2 — выпускают близкие, хотя и не совершенные, субституты и стремятся к максимизации своих индивидуальных прибылей в силу присущей дуополистам обоюдной, двухсторонней взаимозависимости прибыль каждого из них будет функцией не только его собственного выпуска, но и выпуска соперника, так что

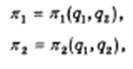
где q1 и q2 — выпуски дуополистов 1 и 2 соответственно.

Тогда условиями максимизации прибылей дуополистов первого порядка будут равенства нулю полных производных функций прибыли (11.3):

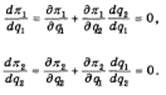
Правые части уравнений (11.4) состоят из двух слагаемых. Первые представляют частные производные функций прибыли по собственным выпускам дуополистов. Вторые слагаемые состоят из двух сомножителей, первый из которых есть частная производная функции прибыли одного дуополиста по выпуску другого; он характеризует взаимозаменяемость их выпусков (с точки зрения величины прибыли каждого из них). Вторые сомножители последних слагаемых правых частей (11.4), характеризуют реакцию второго (первого) дуополиста на решение о величине выпуска, принятое первым (вторым) дуополистом так, как она субъективно представляется первому и соответственно второму субъекту дуополии. Эти сомножители, и представляют предположительные вариации, или, иначе. предположения субъектов количественной дуополии о вариациях выпуска соперника.

Иными будут предположения участников ценовой дуополии. Прибыль каждого из них представляется дуополистам как функция не только установленной им на свою продукцию цены, но и цены, установленной соперником, так что

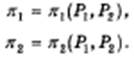
В этом случае условиями максимизации прибылей дуополистов будет равенство нулю полных производных функций прибыли (11.3):

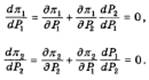
Здесь первые слагаемые правой части представляют частные производные функций прибыли по ценам, устанавливаемым дуополистами 1 и 2 соответственно, а первые сомножители второго слагаемого — частные производные тех же функций прибыли по цене соперника. Наконец, вторые сомножители второго слагаемого (11.4*), характеризуют реакцию второго (первого) дуополиста на решение об уровне цены, принятое первым (вторым) так, как она субъективно представляется первому и соответственно второму субъекту дуополии. Эти сомножители, и представляют предположения дуополистов о вариациях цены на продукцию соперника.

Понятно, что модели дуополии — или в более общем случае олигополии — должны исходить из некоторых гипотез относительно характера предполагаемых каждым субъектом рынка вариаций. Только потом можно говорить об определенности равновесия рынка такого типа и его характеристиках.

11.2. НЕКООПЕРИРОВАННАЯ ОЛИГОПОЛИЯ

11.2.1. КОЛИЧЕСТВЕННАЯ ОЛИГОПОЛИЯ

11.2.1.1. МОДЕЛЬ КУРНО

Впервые модель дуополии была предложена французским математиком, экономистом и философом Лнтуаном-Огюстеном Курно в 1838 г. Мы представим эту модель сначала в числовом виде, а затем дадим более развитую ее аналитическую версию.

11.2.1.1.1. ЧИСЛОВАЯ ВЕРСИЯ

Курно предположил, что существуют две фирмы, каждая из них владеет источником минеральной воды, который она может эксплуатировать с нулевыми операционными затратами. Свой выпуск (минеральную воду) они продают затем на рынке, спрос на котором задан линейной функцией. Каждый дуополист исходит из предположения, что его соперник не изменит своего выпуска в ответ на его собственное решение. Это значит, что, принимая его, дуополист руководствуется стремлением к максимизации своей прибыли, полагая выпуск другого дуополиста заданным .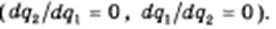

Допустим, что первым начинает добычу воды дуополист 1, так что на первом шаге он оказывается монополистом. Очевидно (рис. 11.1), что его выпуск составит тогда q1, что при цене Р обеспечивает ему максимальную прибыль, поскольку в этом случае MR = МС = 0 • Эластичность рыночного спроса при таком выпуске равна единице, а общая выручка достигает максимума, что при нулевых затратах тождественно максимуму прибыли.

Затем добычу минеральной воды начинает дуополист 2. В его представлении ордината графика на рис. 11.1 сдвинута вправо на величину Оq1 и, таким образом, совмещена с линией Aq1.

Сегмент AD' кривой рыночного спроса DD' он воспринимает как кривую остаточного спроса, которой соответствует кривая его предельной выручки, MR2.

Очевидно, что прибылемаксимизирующий выпуск дуополиста 2 составит половину неудовлетворенного дуополистом 1 спроса, т. е. сегмента q1D'. Значит, величина его выпуска составит q1q2, что обеспечит ему (но тем же, что и дуополисту 1, причинам) максимум выручки и, следовательно, прибыли. Заметим, что этот выпуск составит четверть всего рыночного объема спроса при нулевой цене, OD' (1/2 1/2 = 1/4).

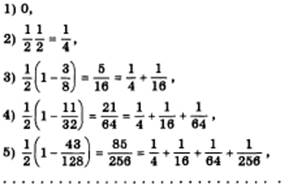
На втором шаге дуополист 1, полагая, что выпуск дуополиста 2 останется неизменным, решит покрыть половину оставшегося все еще неудовлетворенным спроса. Поскольку дуополист 2 покрывает четверть рыночного спроса, выпуск дуополиста 1 на втором шаге составит 1/2(1-1/4), т.е. 3/8 всего рыночного спроса, и т. д. Легко убедиться в том, что с каждым последующим шагом выпуск дуополиста 1, который первым приступил к эксплуатации своего источника и потому сразу же оказался в положении монополиста, будет сокращаться, тогда как выпуск дуополиста 2, «проспавшего» первый шаг, будет возрастать. Этот процесс завершится уравниванием их выпусков, и тогда дуополия достигнет состояния равновесия Курно.

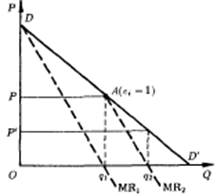
Действительно, при каждом последовательном шаге q1 составит (в долях общего рыночного спроса):

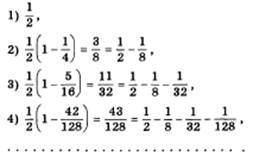
Систему (11.5) можно обобщить, представив выпуск дуополиста 1 в состоянии равновесия, q1, как

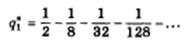или

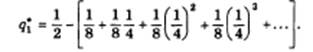
Здесь выражение в квадратных скобках есть не что иное, как бесконечно убывающая геометрическая прогрессия с первым членом q1 и знаменателем 1/4. Тогда равновесный выпуск дуополиста 1 можно определить как разность между 1/2 и суммой членов этой бесконечно убывающей прогрессии:

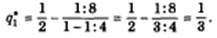
Таким образом, равновесный выпуск дуополиста 1 составит одну треть рыночного объема спроса.

Аналогично можно подсчитать и равновесный выпуск дуополиста 2. При каждом последовательном шаге его выпуск составит:

Выпуск дуополиста 2 возрастает, хотя и в снижающемся темпе. Теперь мы можем представить равновесный выпуск второго дуополиста, как сумму

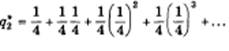
Используя вновь формулу суммы членов бесконечно убывающей геометрической прогрессии, получим

Таким образом, в состоянии равновесия каждый из дуополистов Курно покрывает своей продукцией треть рыночного спроса при единой цене. Покрывая совместно две трети рыночного спроса, каждый дуополист обеспечивает максимум своей, но не отраслевой прибыли. Они могли бы, по-видимому, увеличить свою общую прибыль, если бы, поняв ошибочность своих предположений относительно заданности объемов выпуска друг друга, вступили бы в явный или тайный сговор и действовали как единая монополия (легально или нелегально). В этом случае рынок оказался бы поделенным пополам, так что каждый из них покрывал бы по четверти (вместо трети) рыночного спроса по прибылемаксимизирующей цене.

Курно неоднократно упрекали за наивность его модели дуо­

полии. Модель Курно закрыта, количество предприятий с самого начала ограничено и не меняется в ходе движения к равновесию. Модель ничего не говорит о возможной продолжительности этого движения. Нереалистичным представляется и допущение о нулевых операционных затратах.

Некоторые из этих «врожденных» недостатков могут быть исключены при включении в модель Курно так называемых кривых реагирования. Однако, прежде чем включить их в модель Курно, целесообразно остановиться на важной промежуточной характеристике —кривых равной прибыли.

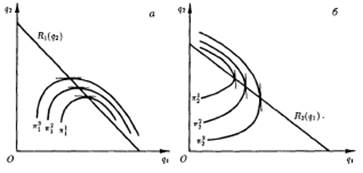
В широком смысле изопрофитами называют множество комбинаций двух или более независимых переменных функции прибыли, обеспечивающих одну и ту же сумму прибыли. В модели дуополии Курно изопрофита, или кривая равной прибыли дуополиста 1, — это множество точек в пространстве выпусков (q1, q2)» соответствующих комбинациям (наборам) выпусков обоих дуополистов, обеспечивающих дуополисту 1 один и тот же уровень прибыли. Соответственно изопрофита дуополиста 2 — это множество точек в том же пространстве, соответствующих комбинациям (наборам) выпусков q1 и q2 обеспечивающих одну и ту же прибыль дуополисту 2. Семейства таких кривых равной прибыли, или изопрофит дуополистов, представлены соответственно на рис. 11.2, а и 11.2, б.

Перечислим кратко основные характеристики и свойства изопрофит.

1. Вдоль изопрофиты величина прибыли дуополиста неизменна.

2. Изопрофиты вогнуты к осям, на которых отображается выпуск того дуополиста, чья изопрофита представлена на рисунке. Так, изопрофиты дуополиста 1 вогнуты относительно оси его выпуска. Такая форма изопрофиты показывает, как дуополист 1 может реагировать на принятое дуополистом 2 решение о величине выпуска с тем, чтобы его уровень прибыли не изменился.

3. Чем дальше отстоит изопрофита от оси выпуска данного олигополиста, тем меньший уровень прибыли она отображает. И наоборот, чем ближе лежит изопрофита к оси выпуска данного дуополиста, тем большему уровню прибыли она соответствует.

4. Для любого заданного выпуска олигополиста 2 существует единственный уровень выпуска олигополиста 1, максимизирующий прибыль последнего. Для дуополиста 1 такой выпуск определяется (при данном выпуске дуополиста 2) высшей точкой на низшей из доступных ему изопрофит.

5. Высшие точки изопрофит дуополиста 1 смещены влево, так что, соединив их одной линией, мы получим кривую реагирования. На рис. 11.2, а R1(q2) — кривая реагирования дуополиста 1 на величину выпуска, предложенного дуополистом 2, а R2(q1) — кривая реагирования дуополиста 2 на величину выпуска, предложенного дуополистом 1.

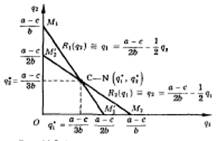
Кривые реагирования — это множества точек наивысшей прибыли, которую может получить один из дуополистов при данной величине выпуска другого. Множества этих точек называют кривыми реагирования, поскольку они указывают на то, как один из дуополистов, выбирая величину своего выпуска, будет реагировать на решение другого дуополиста относительно величины своего выпуска. Нередко, особенно в теоретико-игровых моделях олигополии, кривые реагирования называют кривыми наилучшего ответа. Точка пересечения кривых реагирования обоих дуополистов, совмещенных в одном двухмерном пространстве выпусков, определяет равновесие Курно.

11.2.1.1.2. АНАЛИТИЧЕСКАЯ ВЕРСИЯ

Проведем теперь более строгий аналитический вывод равновесия Курно, отказавшись от ряда сделанных ранее допущений.

Положим, что каждый дуополист (во всех отношениях идентичный сопернику) стремится к максимизации своей прибыли, исходя из предположения, что другой дуополист не будет изменять выпуска, каким бы ни был его собственный выпуск. Иными словами, примем, что предположительные вариации каждого имеют нулевую оценку. Допустим, что обратная функция рыночного спроса линейна:

P = a-bQ, (11.6)

где

Q = q1 + q2- (11-7)

Подставив (11.7) в (11.6), получим

P = a-b(q1+q2). (11.6*)

Тогда прибыли дуополистов можно представить как разности между выручкой и затратами на выпуск каждого из них:

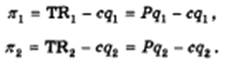
Подставив в правые части (11.8) значение Р, получим

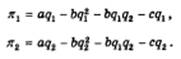
Условием максимизации прибылей дуополистов будет равенство нулю первых производных уравнений:

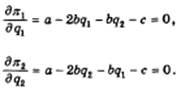
Уравнения (11.10), (11.10*) могут быть переписаны так:

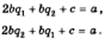
Откуда после несложных преобразований получим

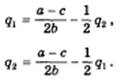
Это и есть уравнения кривых реагирования дуополистов.

После подстановки имеем

и следовательно,

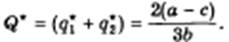
Равновесные выпуски дуополистов (11.13) и являются координатами точки равновесия выпусков Курно—Нэша (точка С—N на рис. 11.3). Говорят, что рынок находится в состоянии равновесия Нэша, если каждое предприятие придерживается стратегии, являющейся лучшим ответом на стратегии, которым следуют другие предприятия отрасли. Или, иначе, рынок находится в состоянии равновесия Нэша, если ни одно предприятие не хочет изменить своего поведения в одностороннем порядке. Такой тип равновесия назван равновесием Нэша в честь американского математика и экономиста, нобелевского лауреата по экономике (1994) Джона Нэша.

Равновесие Курно — частный случай равновесия Нэша, а именно это такой вид равновесия Нэша, когда стратегия каждого предприятия заключается в выборе им своего объема выпуска.

Подставив теперь значения равновесных выпусков из (11.13), найдем значение равновесной цены дуополии Курно:

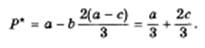
Следовательно, равновесные цены и объемы выпуска дуополистов Курно одинаковы, что объясняется однородностью их продуктов (близостью товаров-субститутов) и равенством их затрат yа производство.

Модель дуополии Чемберлина предполагает, что дуополисты не столь наивны, как в модели Курно, что они способны сделать определенные выводы из собственного опыта. Они не будут, в частности, придерживаться предположения о заданности объемов выпуска друг друга, если видят, что выпуск соперника изменяется в ответ на их собственные решения. И в конце концов они поймут, что в интересах каждого из них действовать так, чтобы их совместная прибыль была бы максимальной.

Таким образом, не вступая в сговор, они придут к желательности установления монопольной цены на свою (однородную) продукцию.

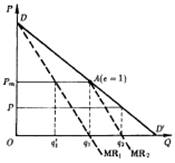
Сходство рис. 11.5 и 11.1 указывает на известную близость моделей Чемберлина и Курно. На рис. 11.5, как и на рис. 11.1, DD' — линейная кривая спроса на продукцию дуополии. Как и в модели Курно (раздел 11.2.1.1), первым начинает производство дуополист 1, его прибылемаксимизирующий выпуск также составит Oq1, что обеспечит ему максимум прибыли (поскольку и здесь MR1 = MC1 = О). Второй дуополист, полагающий в соответствии с допущением Курно, что выпуск первого останется неизменным, воспринимает сегмент AD' как кривую остаточного спроса на свою продукцию. Он попытается максимизировать свою прибыль, покрывая половину остаточного спроса, т. е. q1q2 (поскольку при таком выпуске MR2 = MC2 = О). В результате общий выпуск двух дуополистов составит Oq2, а рыночная цена снизится с Рm до Р.

И здесь в отличие от модели Курно дуополист 1 понимает, что его соперник на самом-то деле (в противоположность его первоначальным предположениям) реагирует на его действия и, по-видимому, будет реагировать и впредь. Тогда он решает вдвое сократить свой выпуск, уменьшить его с q1 до q1^/, который, как легко заметить, будет равен выпуску дуополиста 2. Тогда общий выпуск двух дуополистов будет OQ1, а цена вернется к первоначальному монопольному уровню Рm. Второй дуополист, понимая, что лучше продавать один и тот же выпуск (q1'q1 = q1q2) по более высокой монопольной цене Рm, чем по цене Р, согласится сохранить объем своего производства неизменным. Таким образом, убедившись в своей взаимозависимости, дуополисты добровольно и независимо друг от друга (не прибегая к сговору), выбирают монопольное решение. Поскольку в нашем примере сохраняется допущение о нулевых операционных затратах, рынок окажется поделенным поровну между двумя дуополистами.

Модели дуополии Курно и Чемберлина различаются предположениями продавцов о поведении друг друга. В модели Курно дуополисты при определении своих прибылемаксимизирующих выпусков рассматривают выпуски друг друга как некие заданные параметры, константы. В модели Чемберлина каждый дуополист исходит из предположения о том, что выпуск соперника будет меняться некоторым согласующимся с его собственными интересами образом. Такое предположение в принципе представляется более реалистичным. Ведь при однородности выпускаемой продукции оба дуополиста оказываются, если можно так сказать, «в одной лодке» и действия каждого из них объективно должны быть направлены на то, чтобы удержать «лодку» на плаву и не сбиться с курса. И как любая пара гребцов, они стремятся действовать в унисон.

Однако это предположение отнюдь не бесспорно. Максимизация общей (совокупной) прибыли олигополии (дуополии), весьма проблематична даже при наличии сговора. Тем более она маловероятна в его отсутствии, когда предприятия действуют на свой страх и риск. Ведь для максимизации общей прибыли продавцы должны иметь представление о кривой рыночного спроса и кривых затрат (которые в действительности не являются нулевыми) друг друга.

Иметь одинаковые представления о них при отсутствии сговора вряд ли возможно. Кроме того, как и модель Курно, модель Чемберлина закрыта в том смысле, что она не учитывает возможности входа в отрасль других продавцов. А ведь монопольная цена в дуополии Чемберлина является отличной приманкой для вторжения на ее рынок предприятий-новичков, а тогда равновесие в модели Чемберлина окажется нестабильным. Если вход в отрасль свободен, необходимы дополнительные предпосылки относительно поведения (и взаимоотношений) изначально укоренившихся в отрасли дуополистов и новичков.

Модель асимметричной дуополии, предложенная Г. фон Штакельбергом в 1934 г.представляет развитие моделей количественной дуополии Курно и Чемберлина. Асимметрия дуополии Штакельберга заключается в том, что дуополисты могут придерживаться разных типов поведения — стремиться быть лидером или оставаться последователем.

Последователь Штакельберга придерживается предположений Курно, он следует своей кривой реагирования и принимает решения о прибылемаксимизирующем выпуске, полагая выпуск соперника заданным. Лидер Штакельберга, напротив, не столь наивен, как обыкновенный дуополист Курно. Он настолько изощрен в понимании рыночной ситуации, что не только знает кривую реагирования соперника, но и инкорпорирует ее в свою функцию прибыли. А затем он максимизирует свою прибыль, действуя подобно монополисту.

Ясно, что в случае дуополии возможны четыре комбинации двух типов поведения.

1. Дуополист 1 — лидер, дуополист 2 — последователь.

2. Дуополист 2 — лидер, дуополист 1 — последователь.

3. Оба дуополиста ведут себя как последователи.

4. Оба дуополиста ведут себя как лидеры.

В случаях 1 и 2 поведение дуополистов совместимо, один ведет себя как лидер, другой — как последователь. Здесь не возникает конфликта и исход их взаимодействия стабилен.

Случай 3 по сути представляет ситуацию дуополии Курно, оба дуополиста руководствуются своими кривыми реагирования, и исход их взаимодействия стабилен. Нередко поэтому говорят, что модель Курно — это частный случай модели Штакельберга.

А вот в последнем случае, когда оба дуополиста стремятся стать лидерами, каждый из них предполагает, что соперник будет вести себя в соответствии со своей кривой реагирования, т. е. как монополист Курно, тогда как на деле ни один из них не придерживается такого типа поведения. Исходом подобного взаимодействия становится неравновесие Штакельберга, ведущее к развязыванию ценовой войны. Она будет продолжаться до тех пор, пока один из дуополистов не откажется от своих притязаний на лидерство либо дуополисты вступят в сговор.

Сам Штакельберг считал именно случай 4 наиболее обычным исходом дуополии. Рассмотрим возможные исходы подробнее.

Последователь Штакельберга, как уже было сказано, придерживается своей функции реагирования вида, а затем при определенном количественном решении соперника, представляющегося последователю лидером, приспосабливает свой выпуск к прибылемаксимизирующему уровню. Лидер понимает, что его соперник ведет себя как последователь, и при данной его функции реагирования определяет свой прибылемаксимизирующии выпуск. Поэтому в случае 4 каждый дуополист определяет максимум своей прибыли исходя из предположения, что он является лидером, а соперник — последователем. Если в результате прибыль лидера окажется выше прибыли последователя, дуополист выберет положение лидера, независимо от того, что решит соперник. В противном случае он выберет положение последователя.

Исходя из аналитической версии модели Курно, представим функцию прибыли лидера для дуополиста 1, подставив в уравнение его прибыли функцию реагирования дуополиста 2.Тогда

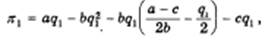
что после преобразований и перестановок дает

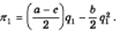
Приравнивая производную по q1 нулю, имеем

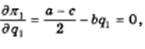
откуда

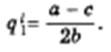
Это и есть оптимальный выпуск лидера Штакельберга. Он обеспечивает максимум его прибыли. В силу симметричности ситуации, возникающей в случае 4, прибылемаксимизирующий выпуск дуополиста 2, тоже претендующего на роль лидера, также составит

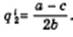
(Верхний индекс / в (11.46) и (11.46*) означает прибылемаксимизирующий выпуск лидера).

Определим теперь прибылемаксимизирующий выпуск последователя Штакельберга:

,

(Верхний индекс f в (11.47) и (11.47*) означает прибылемаксимизирующий выпуск последователя).

Таким образом, прибылемаксимизирующий выпуск последователя, ql, вдвое ниже прибылемаксимизирующего выпуска лидера, ql (i = 1, 2). Заметим, что прибылемаксимизирующий выпуск лидера Штакельберга тот же, что и у дуополиста Курно, а последователя вдвое меньше, чем у последнего.

В случаях 1 и 2, когда один дуополист, неважно какой именно, ведет себя как лидер, а другой как последователь, их общий выпуск будет равен сумме

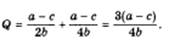
Подставив в функцию рыночного спроса, найдем равновесную цену олигополии Штакельберга в ситуациях 1,2. Она будет равна

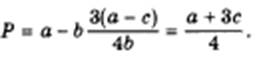
Для того чтобы от равновесия перейти к неравновесию Штакельберга (от случаев 1 и 2 к случаю 4), определим сначала прибыли лидера и последователя. Прибыль лидера, если им окажется дуополист 1, составит

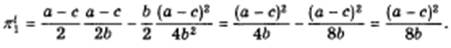
Симметрично прибыль дуополиста 2, если тот окажется лидером, будет

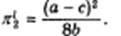
Определим теперь прибыль последователя. Если им окажется дуополист 1, то

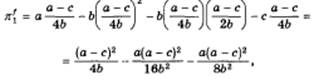
откуда после упрощений и перестановок получим

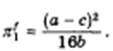
Симметрично прибыль дуополиста 2, если он окажется последователем, будет

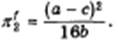
Заметим, что прибыль лидера вдвое превышает прибыль последователя, будь то дуополист 1 или 2. Поэтому-то и тот и другой предпочтут оказаться лидерами. Но тогда их прибыли окажутся не максимальными, а, напротив, минимальными.

Действительно, подставив значения прибылемаксимизирующих выпусков обоих стремящихся стать лидерами дуополистов, в уравнение линейной функции спроса (11.6*),

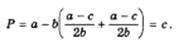
Это равенство цены предельным (и средним) затратам (р = с = МС = АС) означает, что прибыль дуополистпов равна нулю, а это несовместимо со стабильным исходом. Таким образом, ситуация, разрешающаяся стабильным решением в модели Курно, обращается в неравновесие Штакелъберга при некотором изменении предположений о поведении дуополистов. Ниже приведены основные параметры равновесия Штакелъберга:

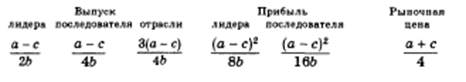
Обычно изучение олигополистического ценообразования начинают с анализа ломаной кривой спроса. Конкуренты не следую г

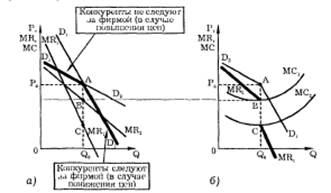
Рис. 8—7. Ломаная кривая спроса 8 1.

Допустим, на отраслевом рынке конкурируют три (I, II и III) фирмы. Рассмотрим реакцию фирм II и III на поведение фирмы I. Возможны две ситуации: когда она повышает цены и когда она их понижает. В случае, если фирма I повышает цены выше Р0 (рис. 8—7а), ее спрос изображается кривой D: выше линии Р0А Конкуренты (фирмы II и III) не будут за ней следовать, и их цены либо останутся неизменными, либо вырастут в гораздо меньшей пропорции, как показывает кривая D выше линии Р0А. При понижении фирмой I цены ниже Р0 фирмы II и III будут следовать за ней, что показывает кривая D: ниже линии Р0А. В результате возникает ломаная кривая спроса D2AD1, высокоэластичная выше уровня текущей цены Р0 и малоэластичная ниже нее (рис. 8—76). Кривая предельного дохода при этом не является непрерывной и состоит как бы из двух участков — MR2 выше точки В и MR1 ниже точки С.

Предложенная модель объясняет относительную негибкость цен при олигополии. Дело в том, что в известных пределах любое повышение цен ухудшает ситуацию. Повышение цены одной фирмой таит опасность захвата рынка конкурентами, которые могут переманить прежних покупателей фирмы, сохраняя низкие цены. Понижение цен в условиях олигополии также может не привести к желаемому росту объема продаж, так как конкуренты, точно так же понизив цены, сохранят свои квоты на рынке. В результате фирма-лидер не сможет увеличить число покупателей за счет других фирм. К тому же понижение цены чревато демпинговой ценовой войной.

Предложенная модель хорошо объясняет лишь негибкость цен, но не позволяет определить первоначальный уровень цен и механизм их роста. Последнее легче объяснить сговором олигополистов.

Стремление олигополистов к кооперативному поведению способствует образованию картелей. Картель — это объединение фирм, согласующих свои решения по поводу цен и объемов продукции так, как если бы они слились в чистую монополию. Образование картеля требует выработки совместной стратегии (по поводу цен, объемов производства), установления квот для каждого участника и создания механизма контроля за выполнением принятых решений. Установление единых монопольных цен повышает выручку всех участников, но рост цен достигается путем обязательного снижения объема продаж. В результате у каждого участника возникает соблазн получить двойной выигрыш, продавать свою продукцию по высокой картельной цене, но с превышением низких картельных квот. Если подобного рода поведение станет всеобщим, то картель развалится.

Картель — классический пример кооперативной игры с п участниками, где п может быть равно 2, 3 и т д Обязательное условие картельного соглашения заключается в том, чтобы каждый его участник получил не меньше того, на что он мог бы рассчитывать при объединении против него всех других олигополистов Часто картельное соглашение предусматривает создание коллективного фонда, из которого осуществляются "побочные платежи" тем, кто пострадал от сокращения квот. Эти выплаты играют роль уравнивающих платежей.

Потенциальную угрозу картелю несет объединение аутсайдеров в контркартель. Если суммарный доход участников отрасли постоянен и равняется максимальной величине, то перед нами — игра двух участников (коалиций) с нулевой суммой, частным случаем которой является модель дуополии по Курно.

Теория игр на ее современном уровне недостаточно учитывает институциональные аспекты цроцесса возникновения, расцвета и упадка картельных союзов. В настоящее время явные соглашения картельного типа встречаются редко. Гораздо чаще можно наблюдать неявные (скрытые) соглашения, тайный сговор.

Тайный сговор — это негласное соглашение о ценах, разделении рынков и других способах ограничения конкуренции, которые преследуются законом.

Если между участниками сговора (всеми продавцами соответствующего рынка) достигнута твердая договоренность, то олигополия вырождается в чистую монополию и все кривые спроса сливаются в одну. Объем продаж определяется точкой В, где MR = МС.

Проекция этой точки на кривую D, т. е. точка А (рис. 8—8), позволяет определить монопольную цену Р0 и экономическую прибыль.

Однако тайный сговор не может быть прочным длительное время. Высокий уровень прибыли и монопольная цена привлекают в эту отрасль новых производителей, что обостряет конкуренцию. Чем больше число участников, тем труднее им договориться между собой. По мере развития производства и насыщения рынка все сильнее сказываются различия в спросе и в издержках производства участников сговора.

Те, кому удалось понизить издержки и повысить спрос, вызывают зависть конкурентов, которым кажется, что их обошли нечестным путем. К объективной дифференциации производителей добавляется субъективный фактор — мошенничество, которое становится заразительным. В обход соглашения осуществляются тайные продажи на льготных условиях. Все эти явления особенно дают о себе знать в условиях спада производства, когда каждый хочет выжить за счет других. Фактором, препятствующим тайному сговору, становится также антимонопольное законодательство.

Поэтому в современном мире чаще всего встречаются не оформленные соглашения (типа картеля), а молчаливая договоренность (типа лидерства в ценах). Обычно движение цен происходит при этом ступенями, причем лидер отрасли (самая крупная или самая технически оснащенная фирма) заблаговременно информирует других производителей (например, через отраслевой журнал) о предстоящем повышении цен Принимая решение, лидер стремится сделать его общеприемлемым, поэтому в отраслях, действующих по этой модели, норма прибыли не максимальна, хотя и выше средней.