Изучение электростатического поля

ИЗУЧЕНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

Все известные в физике взаимодействия - гравитационное, электромагнитное, сильное и слабое - носят полевой характер. Физическое поле, наряду с веществом, является одним из видов материи. Электрическим полем называется вид материи, посредством которого взаимодействуют электрически заряженные тела. Заряженность тел характеризуют величиной заряда тела и обычно обозначают буквой q. Физическую величину, принятую за количественную меру заряженности тел, оцениваемую по способности к электрическому взаимодействию, называют зарядом.

В природесуществуют заряды двух видов, условно называемых положительными и отрицательными. Стабильной частицей, обладающей наименьшим отрицательным зарядом в свободном виде, является электрон; соответственноположительным зарядом – протон. Заряды этих частиц по модулю равны с точностью до 10^-22 (с такой точностью проверена нейтральность атома), остальные же свойства у них различны (например, масса протона m_p превышает массу электрона m_e 1836 раз).

Электрические заряды характеризуются свойствами:

Дискретностью (квантованностью) -электрический заряд любой системы тел состоит из целого числа элементарных зарядов, кратных заряду электрона или протона.

Аддитивностью электрических зарядов – общий заряд Q системы, состоящей из N заряженных частиц, равен алгебраической сумме этих зарядов – Q= 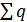_i.

Подчинению закону сохранения зарядов – алгебраическая сумма электрических зарядов тел или частиц, находящихся в изолированной системе, остается постоянной величиной, несмотря на любые взаимопревращения в этой системе.

Инвариантности - независимость заряда тела от скоростиегодвижения, т.е в любой системе отсчета величина заряда данного тела одинакова.

Взаимодействие электрических зарядов q₁ и q₂ есть результат действия электрического поля заряда q₁ на заряд q₂ и, соответственно, электрического поля заряда q₂ на заряд q_{1 (}при этом, одноименные заряды отталкиваются, а разноименные притягиваются). Заряд, всегда является источником электрического поля. Электрическое поле, создаваемое неподвижным зарядом или зарядами, называется электростатическим. Электростатическое поле – частный случай электромагнитного поля и в идеале существует только в инерциальных системах отсчета, где заряды неподвижны, так как любое движение электрических зарядов обуславливает возникновение и магнитного поля.

Основными характеристиками электростатического поля (как и любого другого) являются напряженность и потенциал.

Напряженность электрического поля E в данной точке - это физичес-кая величина, равная силе F, с которой электрическое поле действует на единичный пробный точечный заряд q, помещенный в эту точку

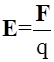(). Пробный заряд - это заряд, собственное поле которого не ис-кажает поле, в которое он помещен. Напряженность - величина векто-рная и является силовой характеристикой поля. Вектор напряжен-ности E имеет направление, совпадающее с направлением вектора си-лы, действующей на положительный заряд в данной точке поля. Согласно закону Кулона, сила F взаимодействия между двумя точечными зарядами определяется по формуле: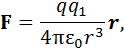

где q₁-заряд создающий поле, q – заряд, на который действует поле, созданное зарядом q₁, r – вектор, соединяющий источник поля (заряд q₁) и координату точки поля расположения заряда q.Тогда, из закона Кулона следует, что напряженность поля точечного заряда определяется по формуле: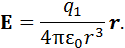

Точечным зарядом называют заряженное тело, размерами которого можно пренебречь по сравнению с величиной r. В системе единиц СИ напряженность электрического поля измеряется в Н/Кл или В/м.

Электрические поля в линейных средах (среды, в которых нет сегнетоэлектриков) подчиняются принципу суперпозиции полей - их независимому сложению: если в данной точке пространства различные заряженные тела создают независимо электрические поля с напряженностями соответственно E₁, E₂,.. En, то вектор напряженности результирующего электрического поля E равен геометрической сумме векторов напряженностей всех электрических полей, т.е E=E₁+E₂+...+En. Чтобы описать электрическое поле в выделенном пространстве, нужно задать вектор напряженности в каждой точке поля. Эту зависимость можно представить не только аналитически, но и графически в виде семейства так называемых линий напряженности (силовых линий ). Линией напряженности электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля в этой точке. Электростатическое поле - источниковое поле: его силовые линии (линии напряженности) не могут пересекаться, они начинаются на положительных и оканчиваются на отрицательных зарядах, или уходят в бесконечность от положительных зарядов и приходят из бесконечности к отрицательным зарядам.

Силовые линии проводятся с такой частотой, чтобы число линий, пронизывающих воображаемую площадку площадью, равной единице и перпендикулярную к силовым линиям было равно значению напряженности поля данной площадке. и поля в данном месте. Следовательно, по густоте силовых линий электрического поля можно судить не только о направлении, но и о значении напряженности поля. Электрическое поле, в котором напряженность одинакова по модулю и направлению в любой точке пространства называется однородным.

Электростатическое поле является потенциальным - это поле, работа сил которого не зависит от траектории движения заряда, а определяется начальной и конечной точками его перемещения, или, работа сил его по любой замкнутой траектории равна нулю.

Как известно, потенциальные поля количественно характеризуются потенциальной энергией. Энергетической характеристикой электростатического поля является потенциал. Потенциалом данной точки поля называют работу по перемещению единичного положительного заряда (q=1) силами поля из бесконечности в данную точку поля. Так как работа носит всегда относительный характер (определяется из какой точки в какую движется тело), то и потенциал любой точки поля зависит от выбора точки отсчета потенциала. Выбор точки отсчета потенциала называют нормировкой потенциала. Нормировка потенциала может быть любой, но чаще всего в физике используют его нормировку относительно бесконечно удаленных точек от источника поля (заряда q₁), принимая потенциал в этих точках за нуль потенциала. В электротехнике за нуль потенциала принимают потенциал Земли или проводника, связанного с ней. Разность потенциалов двух точек поля называют напряжением. Однако, разность потенциалов и напряжение численно равны друг другу только для потенциальных полей, к которым относится и электростатическое поле.

Напряжение и потенциал измеряются в системе СИ в вольтах (В). Потенциалом в 1В обладает точка поля, в которую для переноса заряда в 1Кл силами поля совершается работа в 1 Дж.

Принцип независимого сложения полей (принцип суперпозиции) позволяет рассчитать потенциал поля, создаваемого системой зарядов q₁, q₂,…q_n. Потенциал результирующего электростатического поля в данной точке, относительно выбранной нормировки, равен алгебраической сумме потенциалов полей, созданных каждым зарядом в отдельности: j = j₁+j₂×××+j_n. Потенциал - скалярная величина.

Значение потенциала в каждой точке пространства определяется величиной и конфигурацией заряда, создающего поле, а также расстоянием от источника поля до данной точки. Например, потенциал поля, создаваемого точечным зарядом q в вакууме, относительно бесконечности, определяется выражением: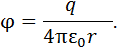

где ε_ο – электрическая постоянная вакуума, r-расстояние от источника поля заряда q до точки, в которой определяется потенциал поля. Если же поле создается протяженным зарядом, то потенциал j в этой точке определится более сложной формулой:

,

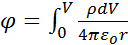где ρ – объемная плотность заряда, V –объем заряженного тела.

Воображаемая поверхность, все точки на которой имеют одинаковый потенциал, называются поверхностями равного потенциала или эквипотенциальными поверхностями. Пользуясь понятием эквипотенциальной поверхности, можно изображать электрические поля графически, подобно тому, как это делается с помощью силовых линий. Пересекаясь с плоскостью чертежа, эквипотенциальные поверхности дают эквипотенциальные линии.

Работа поля по перемещению электрического заряда между двумя точками поля определяется формулой: A= q(j_1-j_2). Из формулы видно, что работа поля по перемещению заряда по эквипотенциальной поверхности равна нулю, т.к. все точки эквипотенциальной поверхности или линии характеризуются одинаковым потенциалом, а _. это значит, что сила, действующая на заряд, все время перпендикулярна перемещению. Отсюда заключаем, что:

1. Л инии напряженности (силовые линии) всегда перпендикулярны (ортогональны) к эквипотенциальным поверхностям (линиям). 2.Эквипотенциальные поверхности (линии) не пересекаются между собой.

Эквипотенциальные поверхности можно провести через любую точку поля, т.е. таких поверхностей можно провести бесконечное множество. Поэтому принято проводить эквипотенциальные поверх-ности (линии) таким образом, чтобы разность потенциалов для любых двух соседних поверхностей была одинаковой (j_i+1- j_i) =const. В этом случае по густоте эквипотенциальных поверхностей (линий) можно качественно судить о величине напряженности поля – чем гуще располагаются эквипотенциальные поверхности тем больше напряженность.

Напряженность и потенциал электростатического поля связаны между собой формулой Е = - gradj. Из формулы следует, что в каждой точке поля вектор напряженности Е и вектор градиента потенциала j равны по величине и противопо- ложны по направлению.

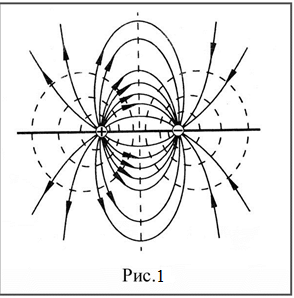
На рисунке 1 сплошными линиями показаны эквипотенциальные линии (сплошные кривые) и линии напряженности (пунктирные кривые) для двух равных разноименных зарядов - диполя.

Из свойств ортогональности силовых линий и эквипотенциальных поверхностей вытекает возможность нахождения поверхности равного потенциала по силовым линиям поля. И, наоборот, по положению эквипотенциальных поверхностей – построение силовых линий поля. Последняя возможность используется в данной работе. Используя связь между напряженностью и разностью потенциалов Е =- gradφ, можно найти величину вектора напряженности на определенном участке поля. Если Δφ- разность потенциалов двух соседних эквипотенциальных линий, а Δx расстояние между ними, измеренное по силовой линии, то пользуясь приближенным соотношением 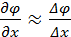по формуле Е= 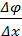можно в однородном поле (или в неоднородном, но на очень малом расстоянии) найти модуль вектора напряженности на участке поля Δx.

В данной работе проводится качественное изучение электростатического поля, графически отображаемое системой эквипотенциальных линий и ортогональной к ним системой линий напряженности поля. Теоретически, как правило, легче производить расчет потенциалов, чем напряженностей поля, так как первые являются скалярными величинами, а вторые – векторными. И экспериментально измерения потенциалов значительно проще, чем измерения напряженностей поля, так как основная часть приборов, применяемых для изучения полей, измеряют разности потенциалов, а не напряженности поля. Поэтому и в данной лабораторной работе экспериментально определяется значения потенциалов в разных точках поля, а не напряженностей. Силовые линии изучаемых полей строятся теоретически как система ортогональных кривых к экспериментально найденным эквипотенциальным поверхностям или эквипотенциальным линиям.

Для изучения распределения потенциалов в работе используется метод зондов. Его сущность заключается в том, что в исследуемую точку электрического поля вводится электрод - зонд. Зонд соединяется с прибором V, измеряющим величину потенциала зонда в данной точке поля относительно потенциала какой-нибудь другой выбранной точки поля, принятой за «нулевое» значение потенциала. При этом необходимо создать такие условия, чтобы зонд принял потенциал той точки поля, в которую он помещен. Только в этом случае показания измерительного прибора, соединенного с зондом, будут отражать правильную картину распределения потенциалов в исследуемом поле. Выполнить это условие в непроводящей среде трудно, что и привело к разработке особого метода изучения электростатических полей путем искусственного воспроизведения их структуры в проводящих средах, по которым пропускается постоянный ток. Следовательно, так как изучение электростатического поля при помощи зондов трудно осуществимо, то экспериментальное исследование электростатического поля заменяют изучением постоянного во времени электрического тока в слабо проводящих средах. Метод изучения электростатического поля путем создания другого эквивалентного ему поля называется моделированием.

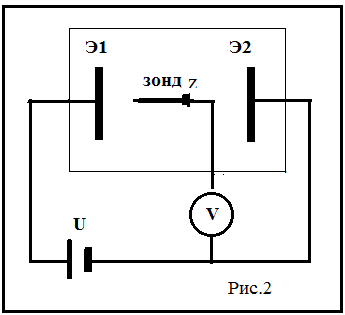
В данной работе проводящей средой является слабый раствор поваренной соли, в которой смачивается лист писчей бумаги. Металлические электроды (Э1 и Э2) различной конфигу­рации устанавливаются на листе бумаги и на них подается постоянное напряжение от источника тока U. В измерительную часть установки входят зонд и цифровой вольтметр V (мультиметр) (рис.2).

Цель данной работы:

1. Экспериментальное исследование электростатического поля в области между заряженными проводниками различной конфигурации и описание его при помощи эквипотенциальных и силовых линий.

2. Рассчитать напряженность поля плоского конденсатора.

ВЫПОЛНЕНИЕ РАБОТЫ:

1.Пропитать в растворе поваренной соли лист бумаги и положить его на плоское стекло.

2.Установить плоские электроды на мокрой бумаге. Положение и форму электродов Э на бумаге отметить «пастовым» карандашом.

3.Включить питание установки. Вольтметром V с помощью зонда Zизмерить потенциал каждого электрода. Определить полярность электродов. Согласно схеме (рис.2) зонд Z на электроде Э2 покажет нулевое значение потенциала, принятое за нормировку (точку отсчета потенциала), а на электроде Э1 – максимальное, равное напряжению источника тока U. Следовательно, электрод Э2 имеет отрицательную полярность, а электрод Э1- положительную.

4.Перемещая зонд вблизи электрода с нулевым потенциалом, с помощью вольтметра найти на бумаге не менее 10 -15 точек с потенциалом 1,50В относительно нулевого. Точки на бумаге отметить пастовым карандашом и подписать значение потенциала. Плавная кривая, проведенная через найденные точки, даст эквипотенциальную линию с потенциалом 1,5В.

5.Выбрав «шаг» изменения потенциала ΔU=0,5 В повторить измерения пункта 4 для потенциалов 2; 2,5; 3; 3,5;4В …вплоть до величины потенциала на электроде Э₁.

6.По указанию преподавателя, пункты 1-5 повторить для других предложенных систем электродов, моделирующих поле точечного заряда, поле диполя, поле сложной системы точечного заряда и плоскости.

7.После просушки листов бумаги, соединить имеющиеся на них точки равного потенциала эквипотенциальными линиями. Построить картину силовых линий (указав их направление) для исследованных пар электродов. Кривые надо стараться проводить не прямо через точки, а так, чтобы они не имели резких перегибов и изломов.

8.В 4-5 точках поля «плоского конденсатора» рассчитать по формуле Е= 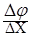модуль вектора напряженности на участке поля Δx. В формуле Δφ- разность потенциалов двух соседних эквипотенциальных линий, а Δx расстояние между ними, измеренное по силовой линии.