Понятие множества используется для описания совокупности предметов и объектов (по Г. Кантору – "многое, определяемое как единое"). При этом предполагается, что объекты данной совокупности можно отличить друг от друга и от предметов, не входящих в эту совокупность.
Отношение принадлежности 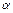 Î
Î  читается "
читается " 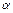 принадлежит множеству
принадлежит множеству  ". Запись
". Запись 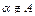 означает, что
означает, что 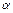 не является элементом множества
не является элементом множества 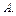 Знак "Î" является стилизацией первой буквы e греческого слова "edti" – есть, быть.
Знак "Î" является стилизацией первой буквы e греческого слова "edti" – есть, быть.
Отношение включения множеств  Í
Í  означает, что каждый элемент множества
означает, что каждый элемент множества  является элементом множества
является элементом множества  . В этом случае говорят, что
. В этом случае говорят, что  – подмножество множества
– подмножество множества  . Употребляется
. Употребляется  равносильная запись
равносильная запись 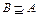 . Множества
. Множества  и
и  называются равными, если состоят из одних и тех же элементов, т.е. (
называются равными, если состоят из одних и тех же элементов, т.е. ( =
=  ) Û (
) Û ( Í
Í  и
и  Í
Í  ).
).
Множество А называется собственным подмножеством множества  , если
, если  Í
Í  ,
,  ¹
¹  . В этом случае пишем
. В этом случае пишем 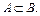 Предполагаем также, что все встречающиеся множества являются подмножествами некоторого универсального множества U.
Предполагаем также, что все встречающиеся множества являются подмножествами некоторого универсального множества U.
Свойства отношения включения:
1)  Í
Í  (рефлексивность);
(рефлексивность);
2) ( Í
Í 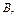
 Í
Í  ) Þ
) Þ  =
=  (антисимметричность);
(антисимметричность);
3) ( Í
Í 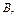
 Í
Í 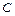 ) Þ
) Þ  Í
Í 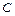 (транзитивность).
(транзитивность).
Если множество  не является подмножеством множества
не является подмножеством множества  , то существует х Î
, то существует х Î  такой, что x Ï
такой, что x Ï  . Но если
. Но если  – пустое множество
– пустое множество 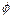 , то такого элемента нет. Поэтому считаем
, то такого элемента нет. Поэтому считаем 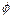 Í
Í  для каждого множества
для каждого множества  .
.
 2015-06-28
2015-06-28 494
494








