Пересечением множеств  и
и  называется множество всех элементов, которые принадлежат
называется множество всех элементов, которые принадлежат  и
и  одновременно, т.e.
одновременно, т.e.
 Ç
Ç  ={ x: x Î
={ x: x Î  и x Î
и x Î  }.
}.
Свойства пересечения:
1)  Ç
Ç  =
=  (идемпотентность);
(идемпотентность);
2)  Ç
Ç  =
=  Ç
Ç  (коммутативность);
(коммутативность);
3) ( Ç
Ç  )Ç
)Ç 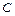 =
=  Ç(
Ç( Ç
Ç 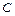 ) (ассоциативность);
) (ассоциативность);
4) ( Ç
Ç  )Í
)Í  , (
, ( Ç
Ç  )Í
)Í  ;
;
5) 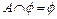 ;
;
6)  Ç
Ç  =
=  Û
Û  Í
Í 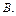
Объединением множеств  и
и  называется множество всех элементов, которые принадлежат
называется множество всех элементов, которые принадлежат  или
или  или
или  и
и  одновременно, т.е.
одновременно, т.е.
 È
È  ={
={ 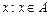 или
или 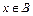 }.
}.
Свойства объединения:
1)  È
È  =
=  (идемпотентность);
(идемпотентность);
2)  È
È  =
=  È
È  (коммутативность);
(коммутативность);
3) ( È
È  ) È
) È 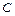 =
=  È (
È ( È
È 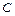 ) (ассоциативность);
) (ассоциативность);
4)  Í (
Í ( È B), B Í (
È B), B Í ( È
È  ) (принцип расширения);
) (принцип расширения);
5)  È
È 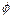 =
=  ;
;
6)  È
È  =
=  Û
Û  Í
Í 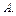
ТЕОРЕМА. 1)  È(
È( Ç
Ç 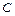 ) = (
) = ( È
È  )Ç(
)Ç( È
È 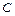 );
);
2)  Ç (
Ç ( È
È 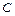 ) = (
) = ( Ç
Ç  ) È (
) È ( Ç
Ç 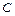 ).
).
Доказательство. 1) 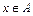 È (
È ( Ç
Ç 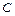 ) Þ
) Þ 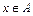 , или
, или 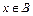 Ç
Ç 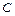 Þ
Þ 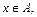 или
или 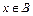 , x Î
, x Î 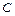 . В обоих случаях по принципу расширения
. В обоих случаях по принципу расширения 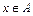 È
È  и
и 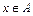 È
È 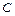 Þ x Î(
Þ x Î( È
È  )Ç(
)Ç( È
È 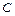 ) Þ (
) Þ ( È(
È( Ç
Ç 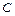 ))Í ((
))Í (( È
È  )Ç(
)Ç( È
È 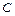 )). Аналогично доказывается включение ((
)). Аналогично доказывается включение (( È
È  )Ç(
)Ç( È
È 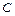 ))Í (
))Í ( È (
È ( Ç
Ç 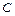 )). Из этих двух включений и следует доказываемое равенство (дистрибутивность объединения множеств относительно пересечения слева).
)). Из этих двух включений и следует доказываемое равенство (дистрибутивность объединения множеств относительно пересечения слева).
Второе утверждение теоремы (дистрибутивность пересечения относительно объединения) доказывается аналогично.
Разностью множеств  и
и  называется множество всех элементов, которые принадлежат
называется множество всех элементов, которые принадлежат  , но не принадлежат
, но не принадлежат 
 \
\  = {
= {  :
: 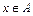 и
и 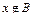 }
}
(в иных обозначениях 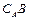 – дополнение
– дополнение  до множества
до множества  ).
).
Свойства разности множеств:
1)  \
\  Í
Í  ;
;
2) ( \
\  ) Ç
) Ç 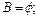
3) ( Í
Í  ) Þ ((
) Þ (( \
\  ) È
) È  =
=  );
);
4)  \
\ 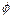 =
= 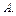
 2015-06-28
2015-06-28 249
249








